Los engranajes del cielo: El planetario opto-mecánico, una joya de la mecánica en vías de extinción (I)

Figura K

Figura L

Figura M

El segundo es un sistema más complejo [Figura L], pero de más fácil construcción. Se trata de un mecanismo de doble manivela o triaxial. Consta de un plato de arrastre primario que arrastra otro plato intermedio, que está desplazado respecto al anterior r/2, a través de unos bulones que deslizan dentro de unas ranuras del plato intermedio (r es el radio del plato y la excentricidad de la órbita del planeta). Este plato a su vez arrastra el plato del planeta, también desplazado r/2, a través de otros dos bulones, de tal forma que la ley de movimiento del último plato es próxima a la de Kepler. Este se conoce como mecanismo de Bauersfeld, que fue su diseñador original, en la fábrica de Zeiss de Jena, Alemania.

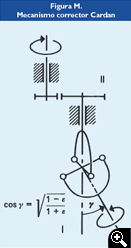
Un tercer sistema es el de transmisión Cardan [Figura M], cuyos ejes no son paralelos, sino que forman un ángulo .

Ese ángulo se elige de tal forma que:

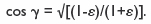
En este caso, dotando al eje de arrastre de una velocidad angular uniforme, el eje de salida da una velocidad variable muy aproximada a la de la ley Kepler, pero con una frecuencia de dos periodos completos por revolución del eje, por lo que hay que añadir un engranaje reductor. Como tiene además el inconveniente del cambio de plano, el sistema se complica bastante y resulta poco práctico constructivamente, aunque es muy preciso.

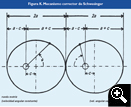
Comparando los errores de los otros dos sistemas, más viables, mientras el segundo puede dar lugar a errores máximos de ±0,05º, el primero, de Schwesinger, lo reduce a ±0,02°. La construcción de éste es complicada, por lo que se suele dotar a los planetarios del sistema de corrección de doble manivela para el planeta de máxima excentricidad, Mercurio y, en algunos modelos, también de Marte, aunque tiene una excentricidad de la órbita (0,093) mucho menor que la de Mercurio (0,206).

En cuanto al error en la velocidad angular debido a la inexactitud en la relación de engranajes, tomando el caso más desfavorable de Mercurio, en el que hay que conseguir un período sidéreo de la exactitud 1/4,15209106, es decir, exacto hasta la cienmillonésima de vuelta, se consigue con bastante aproximación con un tren de engranajes de dientes: 200/20 x 45/65 x 66/91 x 86/104, que da una relación 1/4,15209050, cuya diferencia respecto al valor requerido es de 0,00000056, equivalente a un error de un grado de arco en 5.000 años, aceptable a todos los propósitos.

Proyector de Sol

En el caso del proyector del Sol [Figura N1], el plato de la Tierra es similar al descrito, pero el plato del Sol queda reducido a un punto central, es decir, tiene radio cero y no se mueve. La visual, en este caso se dirige siempre desde el pivote representativo de la Tierra hacia el punto central, del Sol.

La diapositiva para el caso del Sol es un círculo transparente a través del que pasa la luz y se proyecta en la cúpula. Además del disco, se suele simular el halo solar, mediante la difusión o dispersión de parte de la luz del disco en un halo alrededor de la imagen circular. El proyector solar tiene también un filtro de color variable que simula los distintos colores que adopta el Sol según su altura sobre el horizonte, desde blanco, pasando por amarillo, anaranjado y rojo cuando está ya poniéndose. También proyecta un punto de luz difusa en la dirección opuesta al Sol, que se llama anti-Sol, útil para la explicación de los crepúsculos civil, náutico y astronómico, mediante unos círculos paralelos auxiliares proyectados a 6°, 12° y 18° sobre el horizonte.