Los engranajes del cielo: El planetario opto-mecánico, una joya de la mecánica en vías de extinción (I)

Figura I

Figura J

Figura K

Figura L

En la mayoría de los planetarios, la solución constructiva adoptada es montar cada proyector de planetas sobre una barra-guía [Figura H5] que se fija sobre la rótula de uno de los pivotes y que desliza sobre la otra rótula mediante un mecanismo de corredera. Así se consigue que la visual del planeta pase siempre por ese punto, permitiendo a la vez el desplazamiento axial de la barra-guía entre el punto de la Tierra y el del planeta.

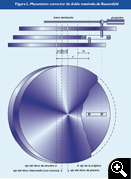
Mediante los piñones [Figura II] situados en la barra de arrastre de “movimiento anual” [I2] se transmite la velocidad de giro exacta, tanto al plato de Tierra [13], como al de planeta [14], que a su vez arrastran el proyector de cada planeta. Así, se pueden simular con suficiente fidelidad sus movimientos relativos vistos desde nuestro planeta, facilitando la comprensión de los bucles de Marte, los de Venus y Mercurio y las retrogradaciones anuales de Júpiter y Saturno sobre el cielo.

El error total en la posición de un planeta, incluyendo holguras y errores de arrastre no puede sobrepasar los 10 minutos en ascensión recta y 1° en declinación, manteniéndose en la mayoría de los casos muy por debajo de estos valores, especialmente en el caso de los planetas exteriores.

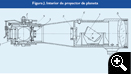
En esencia, el proyector de un planeta es bastante sencillo y es un modelo único para todos los planetas (se suelen representar sólo los 5 planetas visibles a simple vista, el Sol y la Luna). Consta de una pequeña lámpara de bajo voltaje [Figura J1], cuya luz es concentrada por una lente condensadora [J2] hacia una micro-diapositiva de vidrio con la figura del planeta [J3]. La imagen es proyectada mediante un objetivo de óptica larga [J8]. Este proyector tiene interiormente un obturador [J7] auto-orientable por gravedad, que se encarga de atenuar la luz del planeta cuando su imagen se acerca al horizonte y que la oculta por completo cuando baja por debajo de éste.

Hay diferencias importantes para cada planeta en cuanto al montaje, inclinación de platos y mecanismos de corrección de elipticidad de la órbita que se comentan a continuación.

En el caso de Marte, se inclina el plato del planeta 1,85º, y en el de Venus 3,4º, ángulos ya suficientemente acusados para tener que interponer en el tren de engranajes del plato de cada planeta un engranaje de cambio de plano, mediante engranajes cónicos.

El caso de Mercurio es muy especial: además de la máxima inclinación de órbita, de 7,004°, que también requiere un engranaje de cambio de plano, tiene también una elipticidad en su órbita importante (0,206), por lo que no se puede corregir, como en los otros planetas, con un simple desplazamiento del eje respecto al del Sol proporcional a su excentricidad, y es preciso utilizar alguno de los mecanismos que aproximan las posiciones a las predichas por la Ley de Kepler.

Estos mecanismos de corrección son tres principalmente: el mecanismo de los “engranajes elípticos conjugados”, el de “doble manivela” y el “cardan”.

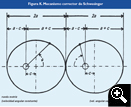
El primero [Figura K], conocido también como mecanismo de Schwesinger, se basa en un par de engranajes en los que las líneas medias de rodadura no son circunferencias sino elipses idénticas conjugadas, dispuestas de tal modo que cuando el punto de engrane se encuentra en el extremo alejado del foco de una de las elipses, en la otra se encuentra en el extremo más cercano al foco. El diseño de los dientes es especial para permitir el engrane en toda la periferia de la elipse. La excentricidad de cada eclipse (c/a) debe ser la mitad de la excentricidad del planeta a representar (/2).

Al mover la elipse de arrastre con velocidad angular uniforme, en la elipse arrastrada se producen aceleraciones y deceleraciones que siguen muy aproximadamente la 2ª ley de Kepler para ese planeta, con un error que se reduce a un término de tercer orden.