El juego de billar ortogonal

Figura 5.

Figura 6.

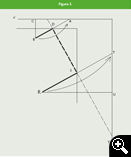
Por ejemplo, el lado emergente del primer ángulo recto es la mediatriz de RR₁ siendo R₁ el primero de los cuatro puntos simétricos de R.

Trazamos la curva Spline que une los cuatro puntos simétricos (cuatro pequeños círculos) y que corta en R´ a la vertical derecha. La mediatriz de RR´ (de trazos) es la línea de plegado buscada.

Comprobación: Al plegar, B cae sobre B´(en la horizontal superior) y R sobre R´ (en la vertical derecha) formándose el trapecio isósceles BB´R´R que a mí me gusta llamar de J. Justin.

Los plegados restantes para conseguir el rectángulo inscrito son inmediatos.

Está claro que, aunque antes cito el Programa CABRI, yo no lo he usado al no disponer de él. Lo que he hecho es generar suficientes puntos mediante Auto Cad para producir la SPLINE correspondiente (Línea de Segmentación Polinómica, con interpolación cúbica) que es el lugar geométrico de los puntos Ri.

Resolución de la ecuación completa de tercer grado

Antes de nada, vamos a fijarnos en la Figura 5 para mostrar cómo en su configuración subyace la ecuación de tercer grado. Esa figura se completa ahora con la siguiente Figura 7 de la que se deducen los valores de t que se muestran a su derecha (tomados valores absolutos).

Vamos a obtener una expresión en t dependiente sólo de las coordenadas de las bolas (0, 0); (l, m), del ángulo de ataque (cuya tangente es t), y de la relación mesa-bolas (a, b):

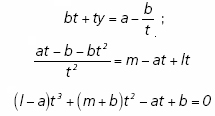
Es decir, la orientación que ha de darse a la bola situada en el origen para que dé en la bola situada en (l, m) después de rebotar ortogonalmente sobre ambas bandas, es la raíz real única de la ecuación de tercer grado que hemos obtenido. Ello se debe a que, para las dimensiones representadas en el dibujo, la ecuación tiene su discriminante positivo.

Es importante insistir en que las dos rectas receptoras en el plegado simultáneo de los puntos Inicio (0, 0) y Fin (l, m) están situadas respecto de las bandas (donde se produce la incidencia de la bola activa) a la misma distancia a que se encuentran de ellas dichos puntos.