El juego de billar ortogonal

Jugada a dos bandas

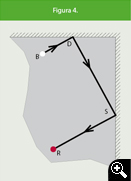
Teniendo las bolas B, R se trata de encontrar la trayectoria de B a R después de golpear las dos bandas. (Figura 4).

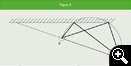
La solución se obtiene (Figura 5):

• Trazando X´ e Y´ paralelas a las bandas por C y U, los simétricos de B y R respecto de dichas bandas.
• Plegando simultáneamente B sobre X´ (produce A) y R sobre Y´ (produce T). Se trata de una doble simultaneidad (dos puntos sobre dos rectas).
• La línea (discontinua) de plegado en valle DS determina el tramo medio del trayecto de B a R.
• Como esa línea de plegado es eje de simetría y la banda por D es paralela media del ABC, el ángulo recto en D se asienta en esa banda horizontal. Otro tanto puede decirse del RTU y la paralela por S a TU.

Jugada a cuatro bandas (billar ortogonal)

Jugar a cuatro bandas con el billar ortogonal equivale a inscribir otro rectángulo en el rectángulo de las bandas. La simulación consistiría en poner una bola en cualquier punto de la mesa e impulsarla con el taco para que, en su camino ortogonalizado chocara con otra bola situada en el mismo lugar que ocupaba la impulsada.

Es decir, se trata de inscribir en el rectángulo de las bandas, otro que pase por un punto cualquiera del interior de la superficie verde.

Mariano Nieto reduce esta situación a la de las figuras 4 y 5 porque el rectángulo inscrito ha de ser concéntrico con el exterior de las bandas y por tanto dicho rectángulo inscrito ha de contener también al punto simétrico del punto dado, respecto de ese centro común. La Figura 6 resuelve el problema como si se tratara de la Figura 5, pero recordando que aquella Figura 5 lo único que hace es dar fe de lo que se obtuvo con el tanteo plegatorio, pero no produce la solución. Ésta la da CABRI (Programa de los Lugares Geométricos), como veremos a continuación.

Sea el punto B en la mesa que produce su simétrico R respecto del centro del rectángulo de las cuatro bandas.

Obtenemos los simétricos de B respecto de la banda superior y de R respecto de la banda derecha. Por estos puntos simétricos hacemos pasar sendas paralelas a las bandas correspondientes.

Por B trazamos cuatro ángulos rectos con sus vértices en la banda superior.

Sucesivamente obtenemos los cuatro puntos simétricos de R respecto de cada lado emergente de aquellos ángulos rectos.