El juego de billar ortogonal
Figura 8.
Figura 9.
Figura 10.
Vamos ya a obtener las tres raíces de una ecuación completa de tercer grado. La expresión está pensada para que su resolución por plegados quepa dentro del papel. Será ésta:
t3 + t2 – 2t -1 = 0
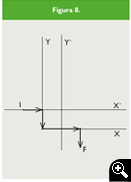
La secuencia de vectores, según coeficientes, será: 1; 1; -2; -1 (Figura 8).
El primer vector con Inicio en I (y valor 1 como el coeficiente de t3) incide sobre la banda Y de manera que exige la línea Y´ para que sobre ella se asiente I en el plegado final.
El segundo vector (valor 1 como el coeficiente de t2) se produce girando a la derecha al finalizar el primer vector (no ha habido cambio de signo al pasar del primero al segundo término de la ecuación).
El tercer vector acusa un giro a la izquierda (hay cambio de signo en el paso del segundo al tercer término de la ecuación) y tiene valor 2, como el coeficiente del tercer término en t.
Como al pasar del tercero al cuarto término de la ecuación no hay cambio de signo, el giro es a la derecha para producir el último vector (valor 1, el del término independiente) que termina en F, el punto Final.
Este último vector viene rebotado de la banda x y exige, por tanto, la línea X´ para asentar sobre ella F en el plegado ulterior. Así pues, habrá de hacerse el siguiente plegado simultáneo:
Lo que ocurre es que este plegado puede hacerse de tres formas distintas dando lugar a la Figura 10.
En ella, las líneas de trazo representan los plegados en valle, y los ángulos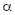 
, 
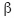y 
conducen a las soluciones de la ecuación.
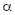= 51,2721º
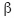= - 23,9909
= - 60,9719
t1 = tg 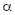= 1,2469
t2 = tg 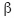= - 0,4450
t3 = tg = - 1,8019
Cualquiera de ellas satisface la ecuación t3 +t2 -2t -1 = 0
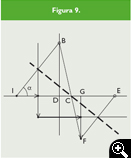
Justificación de que la Figura 8 se asocia a la ecuación de tercer grado propuesta (Figura 9):
En los 
IBD; EGF que son semejantes, se tiene:
 |
 |
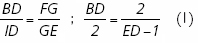
