La vida cotidiana y el aprendizaje

Figura 2.

Figura 3.

Por qué un número double es análogo al rozamiento?

Para empezar a explicar los dos tipos de rozamiento, el estático y el dinámico, es pertinente empezar con el ejemplo más sencillo posible consistente en un bloque de masa m apoyado sobre un suelo horizontal fijo. Al aplicar una fuerza de tracción F sobre el bloque, se pueden dar dos situaciones:

• que la fuerza F sea inferior a la fuerza de rozamiento estático limite

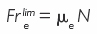
En este caso, el bloque no se mueve, y el rozamiento es estático tomando el valor de la fuerza F: Fr = F

• Si la fuerza F supera el valor de rozamiento estático límite, el bloque comienza a moverse y el rozamiento pasa a ser dinámico con un valor fijo en función del coeficiente de rozamiento dinámico F_r = 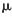_d N

Teniendo en cuenta que el coeficiente de rozamiento dinámico suele ser algo inferior al estático, es posible graficar el valor del rozamiento en función de la fuerza según se indica en la Figura 2.

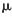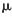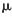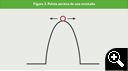
En uno de mis primeros años de docente, un alumno me preguntó qué pasaba si la fuerza de tracción F era exactamente igual a la fuerza de rozamiento estático límite _d N. ¿El rozamiento sería estático y valdría F_r = _e N o sería dinámico con valor F_r = _d N? La pregunta estaba llena de sentido. ¿Las discontinuidades matemáticas producen discontinuidades físicas? Mi respuesta fue que la probabilidad de que la fuerza F fuera exactamente igual a la fuerza de rozamiento estático límite 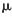_eN es igual a la probabilidad de que uno se encuentre una pelota encima de una montaña tal como se dibuja en Figura 3, es decir, probabilidad nula. Basta con que sople una miaja de viento hacia la derecha para que la pelota se caiga hacia la derecha, o una pizca de viento hacia la izquierda para que caiga hacia la izquierda. En mecánica es lo que se conoce como equilibrio inestable. En el caso del rozamiento, basta con que la fuerza F fuera una pizca mayor que el rozamiento estático límite para que el bloque empezara a moverse y el rozamiento fuera dinámico. Si la fuerza fuera una pizca menor, el bloque estaría quieto y el rozamiento sería estático.

Sin embargo, además de ilustrar este razonamiento con el ejemplo de la pelota encima de la montaña en equilibrio inestable, me pareció conveniente ilustrar este punto con un error que todo programador novel comete alguna vez. He de decir que el error que estoy a punto de mencionar yo también lo cometí en mis tiempos de investigador novel (¡hay que ver cómo pasa el tiempo!), estando un día entero depurando un programa que no funcionaba y la lógica decía que tenía que funcionar. Utilizando el lenguaje de programación C como ilustración, si uno pretende comparar dentro de un programa si dos números reales (también llamados números en coma flotante) doubles de valor 5 son iguales, uno puede pensar en el siguiente código C:

Todo parece indicar que el programa nos saludará adecuadamente cuando lancemos su ejecución. Sin embargo, el desgraciado del programa no saluda ni en pintura. ¿Por qué? Pues porque a no valía 5, valía 4.999999999999999 y b tampoco valía 5, sino 5.000000000000001, con lo cual no eran iguales. Es decir, a era una miaja inferior a 5 y b una pizca superior a 5. Jamás de los jamases dos números doubles pueden ser exactamente iguales1. Lo mismo que en el ejemplo del rozamiento descrito, jamás de los jamases la fuerza de tracción puede ser exactamente igual al rozamiento estático límite, será una miaja superior o una miaja inferior. No se si por suerte o por desgracia, me inclino a pensar que por suerte, la ingeniería no es una ciencia exacta en el sentido exacto de la palabra.