El espacio-tiempo de Einstein

Evidentemente, si sustituimos x y t por sus valores en función de X y de T, obtenidos en elas ecuaciones 4 y 5, la ecuación 3 se convierte, como debía suceder, en una identidad.

Estas relaciones resuelven el problema que nos habíamos planteado y, a partir de ellas, deduciremos fácilmente la contracción en las longitudes y la dilatación en los tiempos apreciados por dos observadores, que tengan entre sí movimiento relativo rectilíneo y uniforme (ambas cosas las utilizaremos más tarde en un ejemplo concreto). En efecto:

a. Si dos puntos de coordenadas X_A y X_B para el observador O, están separados la distancia:

L = X_A-X_B

tales puntos estarán separados para el observador o la distancia:

l= x_A–x_B

y, teniendo en cuenta los valores de x en función de V, de T y de X y de t en función también de V, de X y de T podemos, mediante algunas operaciones elementales, llegar a la expresión:

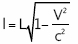
Que representa la contracción del espacio al cambiar de observador. La interpretación de esta contracción del espacio para Lorentz se debía al desplazamiento de las partículas como consecuencia del cambio de movimiento del espacio respecto a cada uno de los observadores; para Einstein, en cambio, se debe a la capacidad del propio espacio para aparecer deformado frente al observador que lo contemple igual que, como veremos a continuación, ocurre con el valor del tiempo ante el fenómeno de su dilatación al pasar de ser visto por un observador a ser medido por otro.

b. Si un acontecimiento desarrollado en un punto dado X del espacio E tiene una duración:

T= T_A-T_B

Tal duración para el observador o valdrá:

t= t_A-t_B

Y, teniendo en cuenta los valores de t en función de V, de X y de T, tendremos:
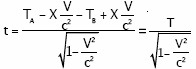