El espacio-tiempo de Einstein

Si ambos observadores asignan valores cero a las coordenadas en su espacio y al tiempo en que se inicia la de partida del rayo de luz podremos escribir que:

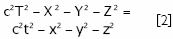
Por lo tanto, y para el caso concreto del estudio de la propagación de la luz tanto analizada por el observador O como estudiada por el observador o, la igualdad anterior será la interrelación entre los valores de las dos cuaternas T, X, Y, Z y t, x, y, z correspondientes a las respectivas expresiones del espacio-tiempo desde el punto de vista del observador O o desde la óptica del observador o.

Encontrar la interrelación entre estas ocho variables teniendo una sola ecuación y las únicas condiciones de conocer el valor de la velocidad de la luz c y el movimiento relativo V entre los dos espacios E y e no es nada trivial.

Vamos a encontrar una solución a este problema particularizando al caso en que la luz únicamente se propagara en la dirección X, coincidente con la dirección x y que la velocidad relativa V entre los dos espacios E y e, además de ser constante, fuera paralela a la dirección de X y de x. En este caso particular, la ecuación [2] se convertiría en:

A partir de esta ecuación determinemos los valores de x y de t para el observador móvil o en función de los valores de X y de T para el observador O, determinación que no es inmediata ya que tenemos una sola ecuación relacionando cuatro variables; no obstante, tenemos otros dos datos (la constancia de la velocidad c de la luz y la condición de que entre los dos sistemas de ejes exista una traslación rectilínea, constante y paralela a los dos ejes X-x de valor V), que nos permitirán superar esta dificultad.

Después de realizar algunos cambios de variables y de realizar una serie de operaciones matemáticas no muy difíciles de desarrollar (el lector interesado puede encontrarlas en un artículo anterior mío en Anales de Mecánica y Electricidad –Aspectos Matemáticos de la Relatividad–) llegamos a establecer que:

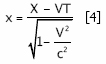
y que:
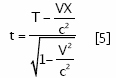