El espacio-tiempo de Einstein

Imaginemos el caso, al que siempre recurrimos, de que tengamos un tren que se mueva con movimiento rectilíneo y uniforme respecto a cualquiera de las estaciones de la vía férrea por la que circule y vamos a considerar como observador o un viajero sentado en dicho tren y como observador O el jefe de una de las estaciones, por las que pase el tren, sentado en su despacho. Es evidente que el observador móvil se mueve respecto al fijo con una velocidad rectilínea y uniforme de valor:

siendo:

X, Y, Z los vectores que representen la posición del viajero o respecto al jefe de estación O.

T el tiempo medido por el reloj del citado jefe de estación.

Sabemos, desde la ya citada experiencia de Michelson-Morley, que la propagación de la luz tiene las mismas características tanto si es juzgada desde O como si es vista desde o y vamos a suponer que:

a. Desde un punto O_S de la estación, cuyas coordenadas respecto a O sean X_S, Y_S, Z_S, emitimos, en el instante T_S, un destello de luz que en el instante T_E, por la igualdad de la velocidad de la luz en cualquier dirección, alcanzará para O los puntos X_E, Y_E, Z_E de una esfera de radio C(T_E-T_S), siendo C la velocidad de la luz en la estación y en todos sus alrededores (en el espacio solidario al observador O). Por lo tanto, podremos escribir:

b. El observador o sentado en el tren, verá que una luz se emite desde un punto cuyas coordenadas para él son x_s, y_s, z_s, en el instante de su reloj ts y alcanza en su instante te los puntos de una esfera x_e, y_e, z_e de radio c(t_e-t_s) sabiendo que c es la velocidad de la luz vista desde el tren. Por lo tanto (en el espacio solidario al observador o) ha de cumplirse igualmente que:

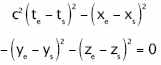
Ahora bien, sabemos desde Michelson-Morley que, a pesar de que exista movimiento relativo entre la estación y el tren, se cumple que:

C = c