El espacio-tiempo de Einstein

i. En los casos g estamos hablando de cierta masa que, con frecuencia, se ha considerado como masa gravitacional y en el ejemplo h de la masa que, a veces, se ha llamado masa inercial pudiendo constatar que ambas son la misma cosa y que nunca ningún experimento será capaz de distinguirlas entre sí.

j. Por otra parte sabemos, por geometría elemental, que la relación entre el perímetro interior del tubo y su radio vale:

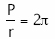
Si una vez girando el tubo pudiésemos saber exactamente, por un lado el valor percibido por nuestro amigo instalado en el tubo para el perímetro interior del mismo y por otro el valor para su radio, ambos valores serían tales que su relación dejaría de ser igual a 2. La razón hay que buscarla en que el radio del tubo, cuando gira, tiene un movimiento relativo, respecto a cuando estaba parado, ortogonal a dicho radio; mientras que, en el perímetro, la dirección del movimiento relativo, cuando gira, respecto a cuando estaba parado, es tangente al cilindro y, por lo tanto, coinciden en dirección el movimiento relativo y el espacio a medir. La Teoría de la Relatividad Especial nos descubre que, cuando existe movimiento relativo entre dos espacios, se produce, al comparar los valores percibidos por un observador para dichos espacios, una contracción del uno respecto al otro en la dirección del movimiento relativo y dicha contracción es nula en la dirección ortogonal a dicho movimiento relativo.

k. Por la equivalencia entre que un sistema tenga un movimiento con aceleración constante o que el mismo esté sometido a un campo gravitatorio constante y uniforme, dos relojes exactamente iguales, situados uno en lo más alto de una torre y otro al pie de la misma, no marcarán exactamente el mismo intervalo de tiempo entre dos hechos concretos; ya que, en la dirección determinada por los dos puntos en que situamos ambos relojes, está actuando el campo gravitatorio terrestre y para un observador aislado del exterior el campo gravitatorio equivale a un movimiento acelerado.

Con todas estas matizaciones Einstein puntualizó la manera como realmente se le presentan, a cada uno de los posibles observadores, los valores del espacio y del tiempo de cualquier movimiento que se pretenda analizar. En este análisis, la mecánica no puede estudiar el movimiento de los cuerpos en el espacio tridimensional rígido de nuestros clásicos en función del tiempo, medidos ambos por cualquier observador, sino que, por estar interrelacionados el paso del tiempo, el espacio recorrido y el movimiento del observador, es necesario utilizar una nueva entidad, función de las tres dimensiones espaciales (x, y, z) y de la dimensión temporal (t), cuyos valores para cada observador serán función del movimiento en estudio y del movimiento relativo entre el observador y aquello cuyo movimiento trate de comprender; es decir, en un medio de cuatro dimensiones (t, x, y, z) tal que en los valores de cada una de estas cuatro dimensiones esté implícito también el movimiento relativo entre el sujeto que pretenda conocer el movimiento y el objeto cuyo movimiento trate de analizar. En este sentido, el tiempo viene a ser una dimensión más del Universo que, como veremos al estudiar con más rigor el problema, siempre vendrá multiplicado por el valor constante de la velocidad de la luz (c), lo que lleva consigo que el tiempo quede asimilado a una variable espacial más. Es evidente que, según esta asimilación, 1 segundo equivale a 3.10⁸ metros.

De todo esto deducimos la necesaria existencia, como preconizó Minkowski, de una nueva identidad geométrica en la que, para cada uno de los observadores, tienen lugar los movimientos, identidad que vendrá definida por un vector s tal que:

s = f(ct, x, y, z)