El espacio-tiempo de Einstein

Para el observador o su espacio-tiempo valdría:

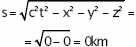
ya que el observador viajando con el fotón pensaría que él estaba en reposo y que la Tierra se aproximaba hacia él a la velocidad c por lo que:

a. La distancia a recorrer por la luz sería nula como consecuencia de la contracción de longitudes antes analizada al pasar de observarla desde O a observarla desde o.

b. La velocidad de la luz también valdría c=3.10⁵ km/seg.

c. Es nulo el tiempo empleado por la luz para recorrer la nula distancia, que o se ha desplazado, en su sistema de referencia. Este tiempo nulo, visto desde o, se convierte en los 500seg para el observador O como consecuencia de la dilatación de los tiempos también antes estudiada.

Comprobamos que el valor del espacio-tiempo se conserva al cambiar de observador y que, por tratarse de la propagación de la luz, como ocurriría con cualquier otra onda electromagnética, el valor del espacio-tiempo para ambos observadores es nulo, de acuerdo con la ecuación [12].

Como en este caso el viajero o (en un fotón) se desplaza respecto a O con una velocidad V = c, el jefe de estación lo verá, por la ecuación [16], desplazarse en su espacio-tiempo con una velocidad de desplazamiento igual a la de la luz y sin envejecer; pero dicho viajero estará convencidos de que no se ha movido.

Nota. Los valores enormes que aparecen, tanto para la contracción de longitudes (al pasar de O a o) como para la dilatación de los tiempos (al pasar de o a O), se deben a que estamos trabajando con la velocidad relativa límite igual a la velocidad de la luz.

Veamos otro ejemplo, que dejamos sin resolver como ejercicio de estudio para el lector, y que podríamos enunciar de la forma siguiente:

Supongamos el observador O del ejemplo anterior sentado en su estación, el observador o₁ también del caso anterior subido en su fotón y un tercer observador o₂ montado en un tren que pasara por la estación, donde se encuentra el observador O, circulando, respecto a O a una velocidad rectilínea y uniforme de valor, evidentemente, muy inferior a c. Encontrar la ecuación del espacio-tiempo para cada uno de los tres observadores y las velocidades de desplazamiento y de envejecimiento que percibirán cada uno de los tres observadores ante cualquier evento que tuviera lugar en alguno de los tres espacios considerados.

Para insistir una vez más en la capacidad de adaptación tanto del tiempo como del espacio, en la identidad geométrica espacio-tiempo, pongámonos ante otra nueva situación. Supongamos los mismos observadores (el jefe de la estación y el viajero del fotón) y que el jefe de la estación contratara pintar una de las paredes de su estación orientada prácticamente en la dirección en que llega la luz, procedente del Sol, a la estación de nuestro problema. Una vez concluido el trabajo, el pintor sugiere al jefe de la estación que le pague por su trabajo según lo percibido por el viajero cabalgando en el fotón. El jefe de la estación acepta y le envía un fax a nuestro viajero solicitándole información para pagarle al pintor. ¿Cuándo opina que recibiría el jefe de la estación la respuesta del fotón y cuál sería en una primera aproximación el sentido de esta respuesta?