Home > Holografía de microondas

Figura 1. “Event Horizont”. Rudie Berkhout.

Figura 2. “Ping-pong”. Dieter Jung.

Figura 3: Harry Potter y Albert Einstein. Fotografías tomadas en tienda Face-Off (se dedican a generar retratos holográficos personalizados en cubos de cristal) ubicada en Via in Arcione (Roma).

Figura 5. Letras ICAI formadas por array de aperturas rectangulares

Figura 6. Apertura rectangular con polarización vertical

Figura 7. Radiación emitida por una apertura cuadrada de lado 4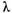 en campo lejano. (n=256 muestras)

Figura 8. Radiación emitida por una apertura cuadrada de lado 4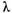 en campo cercano

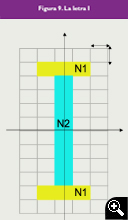
Figura 9. La letra I

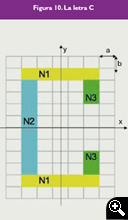
Figura 10. La letra C

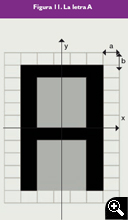
Figura 11. La letra A

Figura 12. Radiación emitida por el objeto de la figura 5 con a=b=5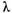

Figura 13. Reconstrucción del objeto radiante de la figura 5 con a=b=5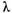. (n=256 muestras)

Figura 14. Otra imagen del objeto radiante de la figura 5 con a=b=5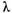.(n=256 muestras)

Referencias
http://www.nobelprize.org http://www.lmsintl.com

Figura 15. Radiación emitida por el objeto de la figura 5 con a=b=0.5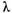. (n=256 muestras)

Figura 16. Reconstrucción del objeto radiante de la figura 5 con a=b=0.5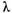. (n=256 muestras)

Figura 17. Radiación emitida por el objeto de la figura 5 con a=b=8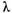. (n=256 muestras)

Figura 18. Reconstrucción del objeto radiante de la figura 5 con a=b=8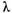. (n=256 muestras)

Figura 19. Radiación emitida por el objeto de la figura 5 con a=b=8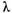. (n=512 muestras)

Figura 20. Reconstrucción del objeto radiante de la figura 5 con a=b=8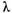. (n=512 muestras)

Palabras clave: Holografía, microondas, ondas planas.

Key words: Holography, microwaves, planar waves.

Resumen: La holografía es un campo de las ciencias físicas que ha permitido el desarrollo de nuevas técnicas y aplicaciones. Presenta un campo de investigación de interés creciente, incluso en el ámbito de las bellas artes. Su descubrimiento se realizó en 1947 por Dennis Gabor, que fue galardonado en 1971 con el Premio Nobel en Ciencia Físicas por dicho hallazgo. Este documento supone una estructura de tres letras conductoras formadas por un ‘array’ de aperturas rectangulares. Corrientes superficiales serán inducidas sobre la estructura, cuando un frente de ondas planas incida frontalmente sobre ella. Las corrientes generarán a su vez un campo eléctrico, cuyo vector de radiación servirá para determinar la forma de las letras.

Abstract: Holography is a Physics field that has developed several new techniques and applications. It shows an interesting research field, even and it is being used in art, so holography can be considered science, art and technology. It was invented in 1947 by Dennis Gabor who was awarded the Nobel Physics Prize in 1971 because of this. This paper assume three letters made up rectangular apertures array, which are head on hitted, by planar waves vertically polarized. Induced surface current is produced and it generates a new electric field, which radiation vector is catched, in order to determine the struture shape.

Autores: José María Sanz Nogales

José María Sanz Nogales Actualmente destinado en el Acuartelamiento Aéreo de Getafe; concretamente en el Centro Logístico de Transmisiones (CLOTRA). Cometidos de Jefe de Escuadrón de Aviónica y Control de Producción del Escuadrón de Sistemas Terrestres. 2010 Ingresó en el Cuerpo de Ingenieros Escala de Oficiales del Ejército del Aire. 2007 Ingresó en el Cuerpo de Ingenieros Escala Técnica Oficiales del Ejército del Aire. 2004 Ingeniero en Automática y Electrónica Industrial por La Universidad Pontificia de Comillas (ICAI). 2002 Ingeniero Técnico en Electrónica Industrial por La Universidad Antonio de Nebrija.

Introducción a la holografía: definición, aplicaciones y orígenes

El Diccionario de la Real Academia Española define holografía de la siguiente manera: “Técnica fotográfica basada en el empleo de la luz coherente producida por el láser. En la placa fotográfica se impresionan las interferencias causadas por la luz reflejada de un objeto con la luz indirecta. Iluminada, después de revelada, la placa fotográfica con la luz del láser, se forma la imagen tridimensional del objeto original.” Según la definición, parece ser necesario el empleo de radiación dentro del espectro visible (desde 384THz hasta 789THz) que sea reflejada por el objeto, y que permita impresionar una placa fotográfica para luego obtener la imagen en 3-D con un láser. Nada más lejos de la realidad; de hecho hoy en día se emplean técnicas holográficas con el fin de obtener imágenes en 3-D a partir de la radiación emitida por un objeto, que no tiene por qué estar dentro del espectro visible. Dicha radiación abarca frecuencias tan dispares como las microondas (desde 1GHz hasta 300GHz), la infrarroja (desde 300GHz hasta 384THz), la ultravioleta (desde 789THz hasta 30PHz) e incluso los rayos X (desde 30PHz hasta 30EHz).

En cuanto a la dimensión artística de la holografía, cabe destacar las exposiciones en el Museo del Hermitage, Museo de Holografía de París y Museo Histórico de Kiev. Sin olvidar las figuras de Rudie Berkhout y Dieter Jung, consideradas como algunas de las más influyentes en el ámbito de la holografía desde el punto de vista artístico.

En cuanto a la dimensión científica y técnica de la holografía, cabría destacar el desarrollo de múltiples aplicaciones en campos tan dispares como medicina, robótica, defensa, telecomunicaciones, aeronáutica, cosmología, geología, geografía, meteorología, acústica, etc. El radar de apertura sintética (SAR), el desarrollo de memorias ópticas, la medida y análisis de la erosión en turbinas de turborreactores, la implantación de modelos acústicos en aeronaves comerciales para aumentar el confort de los pasajeros, la obtención de imágenes 3-D en medicina y cartografía, el análisis de imágenes para teledetección y el desarrollo de teorías cosmológicas, como “el Universo Holográfico”, son solamente algunos ejemplos de sus aplicaciones. La holografía es una realidad que está bien presente en nuestra vida cotidiana; hoy en día, todo el mundo está familiarizado con los hologramas de las cubiertas de libros y CDs, etiquetas, tarjetas y documentos de identificación, tarjetas de crédito, etc [1].

Para hablar de los orígenes de la holografía habría que remontarse al menos hasta el siglo pasado para fijarse en la figura de un ingeniero eléctrico llamado Dennis Gabor (1900-1979). Nacido el 5 de junio de 1900 en Budapest, el joven Dennis Gabor pronto destacó por sus cualidades para la ciencia e ingeniería. Como curiosidad, cabría señalar que en 1911, con apenas 11 años de edad, el pequeño Gabor obtuvo su primera patente: La número 54.703 por su tiovivo de aeroplanos [2]. El invento suponía en aquella época un novedoso tiovivo con aviones motorizados que variaban su altura conforme giraban en torno a un eje central. Más adelante en 1923, obtiene el diploma de ingeniero eléctrico por la Universidad de Berlín. No obstante, aunque Dennis Gabor era ingeniero de profesión, su firme interés y vocación por las ciencias físicas le llevaron a obtener en 1971, el Premio Nobel por el avance que supuso en el campo de la óptica, el invento y desarrollo del método holográfico [3].

Holografía de microondas. Simulación de una aplicación práctica

Ahora bien, por holografía de microondas pueden entenderse todas aquellas técnicas orientadas a la obtención de una representación 3-D de un objeto, en base a la emisión que radia en la banda de las microondas. Para profundizar un poco más en este concepto suponga que se dispone de una estructura conductora constituida por un ‘array’ de aperturas rectangulares que forman las letras ICAI.

Pues bien, cuando un frente de ondas planas proveniente de un radar, satélite o similar incida frontalmente sobre la estructura conductora se producirá una corriente inducida sobre la superficie, que a su vez, generará un campo electromagnético que podrá ser leído con el fin de determinar la forma del objeto que lo emite.

El vector de radiación en cualquier punto del espacio como consecuencia de la aparición de las corrientes superficiales [4] es:

(1)   

Nótese que la expresión del vector de radiación (1) puede entenderse como una transformada de Fourier 2-D de la distribución de corrientes. Este concepto será clave para obtener más adelante la forma del objeto.

Si se particulariza la expresión (1) para el caso de una apertura rectangular homogénea de dimensiones axb, cuando se ilumina con un frente de ondas plano uniforme con polarización vertical, se obtiene que:

(2)   

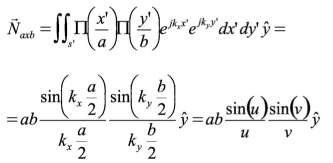
Las siguientes expresiones serán útiles para definir el margen visible de la apertura:

(3)   

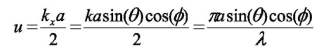
(4)   

(5)   

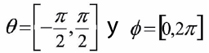
Puesto que: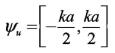   

(véase figura 6)

El margen visible quedará de la siguiente manera:

(5)   

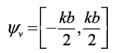
(6)   

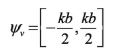
Fuera del margen visible se producirá la propagación de ondas evanescentes cuya intensidad caerá de forma exponencial con la distancia; por tanto, considerar solamente la propagación en el margen visible es análogo a realizar una medida del patrón de radiación de la estructura en campo lejano [5]. Si se realizase una medida en campo cercano, considerándose de este modo ondas evanescentes a parte de las ondas planas, se obtendría una medida de campo radiado con un mayor número de lóbulos en el plano de la frecuencia, que daría lugar a una resolución mayor a la hora de reproducir la forma del objeto radiante. No obstante, el lector comprobará más adelante que con una medida en campo lejano es suficiente para el objeto que persigue este artículo. Las figuras 7 y 8 muestran la representación gráfica normalizada en ejes k_x/k y k_y/k y en escala lineal, del modulo de la radiación emitida por una apertura cuadrada de lado 4, medida en campo lejano y cercano respectivamente.

El siguiente paso consiste en calcular los diagramas de radiación de cada una de las letras compuestas por aperturas rectangulares de dimensiones axb.

(7)   

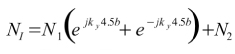
Haciendo uso de la expresión (2) y si el lector permite un abuso en la notación, se tiene que:

(8)   

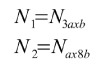
El diagrama de radiación de la letra C puede calcularse de la misma forma que se ha empleado para calcular el diagrama de la letra I.

(9)   

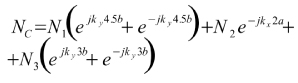
Y ahora:

(10)   

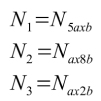
El diagrama de radiación de la letra A puede calcularse suponiendo que es una apertura cuadrada de dimensiones 5ax10b bloqueada en dos zonas cuadradas de dimensiones 3ax4b.

(11)   

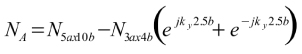
Uniendo las expresiones (7), (9) y (11) se obtiene la radiación emitida por el objeto de la figura 5:

(12)   

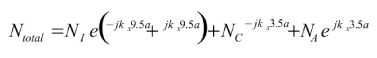
La figura 12 muestra el diagrama obtenido a partir del módulo de la expresión (12) en escala lineal, normalizado y particularizado para a=b=5.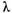

Calculando la transformada de Furrier inversa en 2-D de la expresión (12) se obtiene la forma del objeto que ha emitido tal radiación; ya que como se ha comentado anteriormente, la expresión (1) puede entenderse como una transformada de Fourier de la distribución de corrientes superficiales del mismo objeto1. Las figuras 13 y 14 muestran la forma del objeto obtenida de esta manera.

Suponga ahora que se ilumina el objeto con una señal de frecuencia mucho más baja. Esto es equivalente a reducir la relación que hay entre el tamaño del objeto y la longitud de onda de la señal. Las figuras 15 y 16 muestran lo que sucede cuando a=b=0.5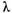. Las gráficas que se obtienen en ambas figuras demuestran que el tamaño de la estructura es tan pequeño en relación con la longitud de onda que se está empleando, que es imposible obtener suficiente información de la radiación que emite el objeto para reconstruir su forma.

Este supuesto, que en principio ha servido para ilustrar un error, podría sin embargo ser utilizado en teledetección, para identificar vía satélite objetivos ocultos como carros de combate camuflados bajo mantas de hojas. En tal caso, las hojas resultarían invisibles, pudiéndose detectar la forma del carro de combate si la relación de su tamaño con la longitud de onda fuera la adecuada.

Si se aumenta en exceso la frecuencia de la señal con que se ilumina el objeto, que es análogo a hacer crecer de manera desproporcionada la relación entre el tamaño del objeto y la longitud de onda que se emplea, se producirá inevitablemente un efecto aliasing que hará imposible la reconstrucción de la forma del objeto. Las figuras 17 y 18 muestran lo que sucede en este caso cuando a=b=8.

Para evitar el efecto aliasing será necesario aumentar la frecuencia de muestreo y emplear filtros anti-aliasing. Las figuras 19 y 20 muestran la mejora sustancial que se obtiene cuando se aumenta la frecuencia de muestreo hasta obtener 512 muestras, en lugar de las 256 empleadas hasta ahora.

Conclusiones

La holografía presenta un vasto campo de aplicación. Se encuentra plenamente integrada en nuestra vida cotidiana y permite el desarrollo de aplicaciones de lo más variopintas.

Las expresiones (5) y (6) demuestran que el margen visible aumenta con la frecuencia de la señal que incide sobre el objeto y radia el mismo. Un aumento del margen visible permite una mejora en la resolución de la imagen del objeto.

La resolución también puede aumentar haciendo medidas de la radiación emitida por el objeto en campo cercano, ya que considera los modos evanescentes de las ondas planas.

Es importante tener en cuenta la relación entre el tamaño del objeto y la longitud de onda de la señal que se va a emplear para iluminarlo. Si la relación es muy pequeña, el objeto no emitirá información suficiente para poder reconstruir su forma. Ya se ha comentado, que esta característica puede emplearse en teledetección para localizar, por ejemplo, carros de combate ocultos bajo mantas de hojas. Por el contrario, si la relación es muy grande, se producirá aliasing y tampoco se podrá realizar la reconstrucción de forma adecuada, a no ser que se aumente la frecuencia de muestreo y se empleen filtros anti-aliasing.

(1) En caso de utilizar MATLAB, será necesario aplicar el comando fftshift después de aplicar la ifft [6].

Descargar este artículo en formato PDF