Home > El fenómeno de "sloshing": una perspectiva computacional sobre la interacción fluido-estructura

Palabras clave: Mecánica de Fluidos Computacional, "sloshing", presión de impacto.
Key words: Computational Fluid Mechanics, sloshing, impact pressure.
Resumen: El fenómeno de "sloshing" se puede definir como el movimiento de la superficie libre de líquidos dentro de contenedores. Esto genera cargas dinámicas en la estructura del tanque y la predicción de esas cargas es un gran reto para la ingeniería.
Para estudiar dicho fenómeno se realiza una simulación numérica con el programa de mecánica de fluidos computacional StarCCM+. Esto permite calcular tanto el campo de velocidades como el de presiones del fluido en el dominio del tiempo y, dado que éste último ocasiona deformaciones en la pared, se producirá una modificación del campo de velocidades y presiones en el fluido por parte de la respuesta de la pared. Es lo que se conoce como la interacción fluido-estructura (o FSI en inglés).
Los resultados de la simulación son contrastados con los de un artículo experimental, lo cual corrobora que éste recoge correctamente la física del "sloshing". Además se estudian computacionalmente otras variables como la respuesta en frecuencia del sólido y su desplazamiento máximo.
Abstract: Sloshing phenomena can be described as the movement of the free surface of liquids inside containers. This creates dynamical loads in the tank structure and the prediction of these loads is an important challenge for engineering.
In order to study the sloshing physics in a fluid tank, a simplified simulation is carried out with the fluid mechanics simulation program StarCCM+. This allows us to compute the velocity and pressure field of the fluid in the time domain. The later leads to wall deformations and the following response of the wall to those deformations in return modifies the velocity and pressure field in the fluid. This is known as a fluid structure interaction case (FSI).
The simulation results are compared against those of an experimental paper, which shows that this captures the sloshing physics accurately. In addition, other variables such as the frequency response of the solid and its maximum displacement are studied computationally.
Autor: Gonzalo Almendral Fernández , Leo Miguel González Gutiérrez, Carlos Ariel Garrido Mendoza

Leo Miguel González Gutiérrez Ingeniero del ICAI (promoción 1996). Licenciado en Ciencias Físicas (UAM 1998). Doctor Ingeniero Industrial por la UPM. Actualmente es profesor en la E.T.S.I Navales U.P.M.

Carlos Ariel Garrido Mendoza Ingeniero Mecánico. Master en Tecnología Energética para el Desarrollo Sostenible. Actualmente es doctorando en la E.T.S.I. Navales U.P.M. en temas de interacción fluido-estructura.
Introducción
Los fenómenos de "sloshing" son de gran importancia en la industria del petróleo y el gas, especialmente al diseñar y operar tanques de LNG. Debido al crecimiento del mercado de gas natural hay un interés creciente en sistemas de producción, carga y almacenamiento para desarrollos "off-shore". También lo hay en tanques de regasificación y plantas diseñadas para evitar la necesidad de construir grandes centrales de procesamiento y distribución en tierra.
Los nuevos retos en metaneros de LNG son el gran crecimiento del tamaño del barco (de 140.000 m3 se ha de pasar a 175.000-250.000 m3), rutas con condiciones climatológicas muy severas (como la que atraviesa el mar de Barents o el Atlántico Norte) y la necesidad de operar con niveles de llenado de los tanques menos restrictivos. En este contexto tiene un gran interés la predicción de cargas causada por los fenómenos de "sloshing" violentos en los tanques de almacenamiento.
Existen dos cuestiones principales en este campo cuya complejidad crece considerablemente cuando el comportamiento del fluido en el tanque pasa a ser no-lineal, incluyendo olas rompientes sobre la superficie. Por una parte, las cargas en la pared necesitan ser calculadas para diseñar adecuadamente los tanques. Por otra parte, la estabilidad del sistema compuesto por el barco y el líquido del tanque ha de estudiarse.
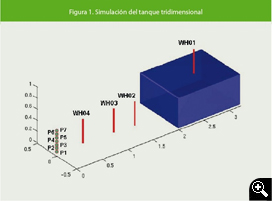
Figura 1. Simulación del tanque tridimensional

Figura 2. Dispositivo experimental usado para la comprobación de la simulación
Por tanto, para diseñar un nuevo tanque de LNG es necesario evaluar el impacto producido por los fenómenos de "sloshing" y analizar la respuesta estructural. Un estudio dinámico de análisis estructural, considerando la interacción fluido-estructura (FSI), es crítico para el estudio de la seguridad.
Las técnicas de modelado existentes actualmente son múltiples [1]. La más sencilla es realizar una analogía con un sistema mecánico. Otras técnicas consisten en tratar el flujo como potencial o aplicar la teoría de aguas poco profundas. Más recientemente se aplican complejos códigos numéricos para resolver las ecuaciones de Navier-Stokes, que rigen el movimiento del fluido. Esta disciplina se conoce bajo el nombre de Mecánica de Fluidos Computacional (CFD en inglés).
Concretamente, el programa StarCCM+ realiza una discretización de las ecuaciones mediante el método de los volúmenes finitos (FVM en inglés), que consiste en dividir el volumen en múltiples "celdas" y aplicar en cada una de ellas las ecuaciones discretizadas de conservación de la masa y la cantidad de movimiento. A esto se le une el método del volumen fluido (VOF en inglés) para capturar la superficie libre del tanque. Dicho método fue desarrollado por Hirt y Nicols [2].
Existen también multitud de estudios experimentales de "sloshing" en el campo naval [3]. Sin embargo, las ventajas de una aproximación computacional saltan a la vista: mientras que un estudio experimental sólo arroja un conjunto discreto de datos, los métodos computacionales permiten conocer las variables de velocidad y presión en todo el espacio e instante.
Debido a esto se usa StarCCM+, un programa comercial muy utilizado en la industria para la simulación de problemas de mecánica de fluidos. Se ha elegido frente a otros códigos por las facilidades de mallado que presenta, por las posibilidades de paralelización del código y por la robustez del mismo. Adicionalmente, permite controlar la convergencia de la solución.
En cuanto a la simulación realizada, se trata del caso de un "Dam-Break" en 2D en el interior de un tanque. Dicho caso consiste en dejar evolucionar bajo la acción de la gravedad a una masa de agua inicialmente confinada en equilibrio hidrostático, a la que se retira la pared interior derecha que la contiene. El agua fluye e impacta en la pared situada en el extremo derecho del tanque.
La simulación del "Dam-Break" en 2D tiene gran interés, al ser los perfiles de ola y las presiones de impacto hasta cierto punto significativas de lo que ocurre en un tanque tridimensional al aparecer "sloshing". La interacción fluido estructura es estudiada modelando la pared que recibe el impacto como un sólido elástico lineal.
Metodología
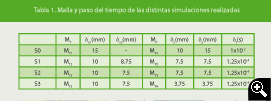
Tabla 1. Malla y paso del tiempo de las distintas simulaciones realizadas
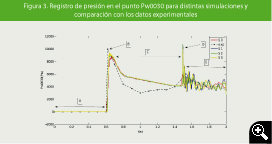
Figura 3. Registro de presión en el punto Pw0030 para distintas simulaciones y comparación con los datos experimentales
El estudio realizado trata de simular la interacción fluido estructura que se produce en un fenómeno de "Dam Break". Para ello la simulación numérica será capaz tanto de introducir las ecuaciones que simulan el comportamiento del fluido y añadir a las mismas las que simulan el comportamiento elástico de la pared de impacto. Todas estas ecuaciones jntas integradas en el dominio del tiempo dan lugar a un problema acoplado de cierta complejidad donde hay presencia de no linealidad proveniente del comportamiento del fluido. Para verificar si los resultados de nuestra simulación son correctos se ha buscado un precedente experimental [4] y se han fijado las dimensiones de nuestra simulación iguales a los del experimento. En el mismo se miden las presiones de impacto en una pared elástica de plexiglás (![]() =1.150 kgm-3, E=3.3 Gpa) impactada por el agua proveniente de un "Dam Break". Una de las diferencias más importantes entre nuestra simulación y el experimento es que en nuestro caso se ha hecho una hipótesis de bidimensionalidad para reducir la carga computacional del problema, asumiendo pocas diferencias en el plano medio de medida respecto al caso 3D.
=1.150 kgm-3, E=3.3 Gpa) impactada por el agua proveniente de un "Dam Break". Una de las diferencias más importantes entre nuestra simulación y el experimento es que en nuestro caso se ha hecho una hipótesis de bidimensionalidad para reducir la carga computacional del problema, asumiendo pocas diferencias en el plano medio de medida respecto al caso 3D.
El tanque tiene altura H = 1 m, largo L = 3,22 m y ancho A = 1 m. En él se encuentra la columna de agua de longitud Lw = 1 m y Hw = 0,55 m. La disposición de la columna de agua en la simulación del artículo puede verse en la Figura 1, en la que además se observan los puntos de obtención de datos de la altura del agua (WH01 a WH04) y los de la presión en la pared (P1 a P7). El modelo experimental puede apreciarse en la Figura 2.
El dato experimental de la presión en el punto P1 para un tiempo menor de dos segundos, situado a z = 0.003 m del fondo del tanque es el que se usa para validar la simulación. Dicho punto pasa a denominarse Pw0030 para hacer referencia a su cota.
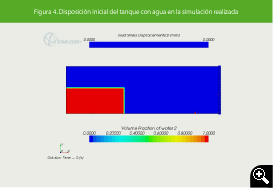
Figura 4. Disposición inicial del tanque con agua en la simulación realizada
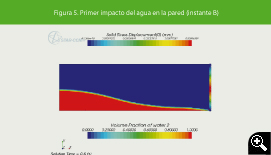
Figura 5. Primer impacto del agua en la pared (instante B)
En una primera simulación se toma un tamaño de malla de x = 0.015Lb = 15 mm, tanto en la malla del interior del tanque como en la de la pared, aunque en esta última, debido a su reducido espesor (10 mm), se obtiene una malla asimétrica de ![]() x = 10 mm y
x = 10 mm y ![]() y = 15 mm. La frontera del sólido ha de tener el mismo número de nodos que la parte de la región fluida con la que está en contacto. Este ensamblaje de mallas permite prescindir de la interpolación para obtener los valores de tensión del sólido con una mayor precisión.
y = 15 mm. La frontera del sólido ha de tener el mismo número de nodos que la parte de la región fluida con la que está en contacto. Este ensamblaje de mallas permite prescindir de la interpolación para obtener los valores de tensión del sólido con una mayor precisión.
El paso de tiempo se fija en ![]() t = 0.001s. Este valor se ha obtenido a partir de casos similares resueltos con StarCCM+ y garantiza que se cumpla la condición de Courant-Friedrich-Levy (CFL), que en una dimensión queda enunciada de la manera siguiente:
t = 0.001s. Este valor se ha obtenido a partir de casos similares resueltos con StarCCM+ y garantiza que se cumpla la condición de Courant-Friedrich-Levy (CFL), que en una dimensión queda enunciada de la manera siguiente:
![]() (1)
(1)
Donde u es la velocidad del fluido en una celda fluida y ![]() x el tamaño de malla. Esta condición asegura la estabilidad del método numérico.
x el tamaño de malla. Esta condición asegura la estabilidad del método numérico.
A continuación se procede a reducir el tamaño de malla hasta conseguir uno a partir del cual la solución no varíe. Se dice que entonces se ha convergido en malla y por lo tanto la solución obtenida es independiente de la malla empleada. Paralelamente se reduce el paso de tiempo favoreciendo la estabilidad hasta que se obtiene la convergencia en paso de tiempo. Las diferentes simulaciones con sus mallas y pasos de tiempo se pueden ver en la Tabla 1, refiriéndose las letras T y P a tanque y pared, respectivamente, y los números a los sucesivos tamaños de malla y pasos temporales empleados
Resultados
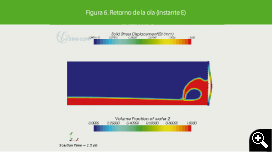
A la vista de la Figura 3 puede establecerse la sucesión de acontecimientos. El agua tarda t = 0.6s en recorrer el espacio que la separa de la pared (A). Tras producirse el impacto se ocasiona un máximo en la presión (B). Posteriormente, la presión se reduce hasta t = 1.48s (C), momento en el que se produce otro pico de presión (D), debido al retorno de la ola generada. La presión sigue descendiendo hasta el final de la serie en t = 2s (E).
Esto se confirma en las imágenes obtenidas en la simulación (ver Figuras 4, 5 y 6). En la Figura 4 se muestra el tanque en el estado inicial. Mientras, en la Figura 5 puede verse el instante del primer impacto (B) a los 0.6 segundos de simulación. Obsérvese que la ola impacta en la esquina inferior, como cabrá esperar es donde está el sensor de presión, luego el primer pico de presión determina el primer impacto en la pared. En la Figura 6 puede apreciarse el instante t = 1.5 s, momento en el que toda la masa de agua ha llegado a la pared y empieza a retornar (D), instante que coincide con el máximo de la deformación, que ocurre en el punto medio como puede verse en la Figura 7, en la que se muestra el desplazamiento del punto medio de la pared en función del tiempo con el máximo de este desplazamiento en cada instante.
En la Figura 3 también puede verse la comparación de la presión en Pw0030 para las distintas simulaciones realizadas. Los valores en A y B convergen muy bien al valor experimental, mientras que en D existe un pico de presión en los datos computacionales que no aparece en los experimentales y que es un 83% superior al valor experimental registrado.
Más llamativa es la discrepancia en el valor en D, que es mucho más elevado que el experimental (e incluso presenta un valor mayor que el primer pico). Estas diferencias podrían ser explicadas a partir de la hipótesis de bidimensionalidad impuesta en nuestra simulación o las diferencias obvias que se producen a nivel experimental cuando se libera la masa de agua.
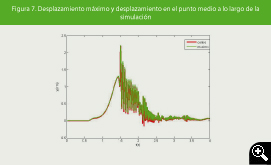
Figura 7. Desplazamiento máximo y desplazamiento en el punto medio a lo largo de la simulación
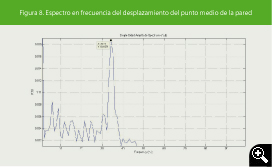
Figura 8. Espectro en frecuencia del desplazamiento del punto medio de la pared
Por otra parte, los valores en E muestran una buena convergencia al valor experimental y una oscilación creciente. Esto es razonable dado que la respuesta vibratoria de la pared va afectando progresivamente a los registros de presión del fluido.
Por último, se procede a validar la respuesta del sólido. Para ello se estudia su respuesta natural en frecuencia. Como puede verse en la literatura sobre vibraciones [5], para una viga empotrada el primer modo de vibración natural viene dado por:
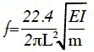 (2)
(2)
Siendo L la longitud de la viga, E el módulo de elasticidad, I el momento de inercia y m la masa por unidad de longitud. Dicha fórmula arroja un valor teórico de f = 34.58Hz. Para poder estudiar la correspondencia del valor teórico con el experimental se analiza el desplazamiento en el punto medio de la pared para 3 < t < 4s. A partir de dicho instante el agua en el tanque se encuentra prácticamente en reposo y las presiones han convergido a su valor hidrostático.
Para ello se halla la FFT (Fast Fourier Transform o transformada rápida de Fourier) a la señal del desplazamiento del punto medio de la Figura 7, obteniéndose un máximo local en f = 34.18Hz, valor muy próximo al teórico. La amplitud de dicho modo de oscilación es de 0.018 mm que se corresponde con el obtenido en la simulación (ver Figura 8). Por todo ello se puede inferir que la física de la pared está bien simulada.
Conclusiones
- Se ha empleado con éxito un "solver" matemático que tiene incorporado el programa StarCCM+, que tiene la ventaja de que se pueden tratar las físicas del fluido y el sólido con la misma formulación matemática, sin necesidad de tener que acoplar códigos.
- Teniendo en cuenta el único dato comparable del que se dispone, la presión en el punto Pw0030, las simulaciones realizadas convergen razonablemente a los valores experimentales excepto para el segundo pico de presión.
- La convergencia de la mayor parte de los datos, junto con su correspondencia con las imágenes obtenidas en la simulación y la validación de la frecuencia de la pared, hace que se pueda constatar que la simulación está correctamente diseñada, obteniéndose un buen acuerdo entre la mayor parte de los valores numéricos y los experimentales.
Agradecimientos
Quiero agradecer a Antonio Souto su ayuda y eficaz dirección en el proyecto fin de carrera del que se origina este artículo. También me gustaría mencionar a Patricia Izaguirre y a José Luis Cercós por su inestimable ayuda.