Home > Un simulador mecánico astronómico del siglo II a.C. El mecanismo de Antikythera

Palabras clave: simulador astronómico, tecnología griega, engranajes diferenciales, mecanismo de Antikythera.
Key words: astronomic simulator, Greek technology, differential gears, Antikythera mechanism.
Resumen: En el año 1900 se descubría un complicado mecanismo del siglo II a.C., en un barco hundido en el fondo marino cerca de la isla griega de Antikythera. En ese barco había un gran tesoro: estatuas de bronce y mármol, ánforas, monedas... y un mecanismo que parecía ser de origen posterior, por su aspecto. Durante 100 años, los investigadores han ido descifrando su finalidad y funcionamiento, pero sólo en 2005, mediante una tomografía en 3D, han podido conocer el número de dientes de todos los engranajes, la forma de cada taladro, remache, unión de "cola de milano", eje, casquillo, y la mayoría de los textos grabados en el material de bronce del que está construido. Diferentes estudios han descubierto que el "mecanismo de Antikythera" era un computador analógico mecánico, del siglo II a.C., que calculaba posiciones astronómicas de los cuerpos celestes con errores de sólo 1/40.000. Mediante técnicas de tomografía avanzadas, su estudio ha puesto la tecnología griega de engranajes de precisión en un lugar mucho más elevado del que se creía hasta ahora.
Abstract: In the year 1900 a complex mechanism from the IInd century B.C. was discovered in a ship wreck near Antikythera Island, Greece. A great treasure was found on the ocean bed: bronze and marble statues, amphorae, coins... and what it seemed to be a mechanism of recent origin. During 100 years researchers have tried to decipher its purpose and the way it worked, but only in 2005, by means of X-ray 3D tomography, they could know the exact number of teeth of all gears, the shape of every drilled hole, rivet, dovetail union, shaft, sleeve and the texts engraved in bronze. Different studies have discovered that the Antikythera mechanism was an analogical computer for astronomical calculations built in the IInd century B.C. with errors of only 1/40.000. With 3D, X-ray advanced tomographic techniques, its study has placed Greek gear technology in a much higher place than it has been thought before
Autores: Juan Antonio Bernedo Casis

Juan Antonio Bernedo Casis Ingeniero Superior del ICAI (promoción 1976), especialidad Mecánica. Jefe Técnico del Planetario de Madrid desde 1987. Miembro del Comité Tecnológico del IPS (Internacional Planetarium Society). Divulgador de Astronomía.
Introducción

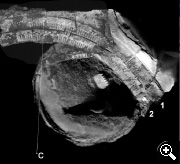
A. Fragmento A visto de frente. Pueden apreciarse los engranajes, remaches, ejes y otras piezas.
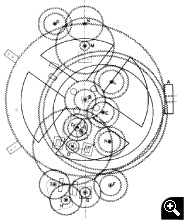
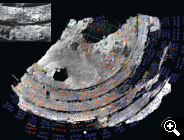
B. Esquema de los engranajes del mecanismo de Antikythera. Fuente Tony Freeth (AMRP, 2008).

C. Cabeza de filósofo. Bronce, 243 a.C.
El mecanismo de Antikythera viene sorprendiendo a los científicos desde su descubrimiento. Su capacidad para predecir eclipses y las posiciones del Sol y la Luna con notable exactitud, fases lunares, calendario e incluso la fecha de comienzo de las olimpiadas principales del mundo antiguo griego, ha sido descubierta poco a poco a lo largo del último siglo. La precisión de sus mecanizados hizo difícil creer que se trataba de un objeto de 2.100 años de antigüedad, pero finalmente la evidencia triunfó. Pruebas de la existencia de un objeto así se encuentran en varias crónicas de Cicerón y otros autores clásicos y han obligado a aceptarla y a reconsiderar el desarrollo de la tecnología de la Grecia clásica, que se creía incapaz de construir objetos como este.
Engranajes de precisión de perfil triangular tallados a mano, ejes coaxiales, engranajes diferenciales, sistemas de arrastre no lineales, deslizaderas y mecanismos de lectura en espiral hacen de éste un mecanismo singular que incluye muchas técnicas de representación mecánica que aparecieron mucho después y algunas sólo muy recientemente. Todo ello habla de un tiempo en el que el conocimiento necesario para calcular y construir estos mecanismos se perdió, hasta los siglos XVII y XVIII en que comenzaron a reaparecer mecanismos parecidos en forma de relojes astronómicos.
El descubrimiento
Este mecanismo ha llegado hasta nosotros gracias a dos tempestades marinas separadas por 20 siglos. La más reciente, en la primavera del año 1900, obligó a un barco griego de buscadores de esponjas, que volvía de la costa africana, a refugiarse en una bahía de Antikythera, una isla del mar Egeo. A la mañana siguiente, ya pasada la tormenta, uno de los buzos descubrió un barco antiguo hundido a una profundidad de unos 50 metros. En el otoño siguiente, ya con patrocinio estatal del Museo Arqueológico de Atenas, se recuperó el gran tesoro artístico que transportaba ese barco, posiblemente botín de guerra con destino a Roma, y que se hundió hacia el año 60 a.C. debido a la primera tempestad de la que hablábamos. Se recuperaron estatuas de mármol y bronce (dos de las mejores esculturas de bronce de toda la antigüedad: la Cabeza de filósofo del 243 a. C. y el Efebo de Antikythera, del 340 a.C.) además de ánforas, monedas y útiles de todo tipo.
Junto a todas esas piezas importantes había un mecanismo de aspecto moderno (A) envuelto en restos de una caja de madera, que pensaron correspondía a un vertido reciente. Sin embargo, la corrosión del bronce y la posición (aplastado bajo las tablas del barco) decidieron a los científicos a considerar que se trataba de algo de la misma época que los objetos hallados en el barco, es decir, al período entre el siglo IV y el I antes de nuestra era.
Primeros estudios
Unos meses después, ya en el Museo Arqueológico de Atenas, se abrió la cubierta calcárea y de óxido, al ir secándose, y el interior de bronce se separó en varios fragmentos, dejando ver algunos engranajes internos y algunas inscripciones de índole astronómica.
El estudio posterior indicó que las inscripciones eran en griego antiguo, de alrededor del año 150-100 a.C. y que los engranajes eran de dientes equiláteros triangulares, a 60o, tallados y mecanizados, como todas las demás piezas, de una misma plancha de bronce, de unos 2 mm de espesor. El mecanismo presentaba ya varias reparaciones, incluyendo la sustitución de uno de los dientes.
Todo ello implicaba la existencia de herramientas y maquinaria de alta precisión que no se creía que existieran en su época, por lo que el descubrimiento siguió en duda, aunque se siguió investigando.
Se aventuró una primera hipótesis de que se trataba de un astrolabio de engranajes, pero mucho más complicado que los primeros de los que se tiene noticia, datados hacia el año 1000 d.C.
Primeros resultados prometedores
En la década de 1950 resultó evidente que el mecanismo era muy complejo y que podía tratarse de una calculadora mecánica astronómica, según estudios de un historiador de la ciencia, de Reino Unido, Derek de Solla Price, que publicó un primer artículo en Scientific American, en 1959. Posteriormente, en 1970, hizo radiografías y gammagrafías de las tres piezas principales (hay hasta 82 fragmentos en total). Descubrió que había unos 30 engranajes y pudo explicar la finalidad de 12 de ellos, que usaban engranajes epicicloides para restar el movimiento aparente del Sol, del mes sidéreo para calcular el mes sinódico.
Es decir, en el siglo II a.C. ya se conocían y utilizaban los engranajes diferenciales. Posteriormente se han hallado otros casos de uso de engranajes diferenciales en el imperio chino, de época algo posterior (150 d.C.) como el Carro que apunta hacia el sur (D), una brújula de ruta que, una vez orientado al comienzo del camino, mantenía siempre la misma dirección aunque girara el carro. Eso implica que esos mecanismos ya se aplicaban ampliamente en la antigüedad.
Curiosamente, también se han descubierto recientemente engranajes helicoidales dobles (E) en las tumbas chinas de Xian, del año 50 d.C. Estos engranajes se "reinventaron" en el siglo XX para la industria de automoción. También son conocidos los engranajes triangulares de Arquímedes (287-212 a.C.), anteriores al mecanismo, así que es perfectamente verosímil su origen tan antiguo.
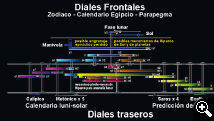
Derek de Solla Price amplió el estudio y construyó un modelo con dos diales traseros, que incluían varios tipos de calendarios, y uno frontal, que podía predecir las posiciones del Sol y la Luna, y las horas de salida y puesta de estrellas y constelaciones importantes. Este esquema aún perdura en los modelos más recientes y evolucionados. Este investigador ya se dio cuenta de las implicaciones del descubrimiento, y advirtió: "Si es genuino el mecanismo de Antikythera, habrá que reevaluar toda la tecnología griega. Su descubrimiento es tan importante como el de la tumba de Tutankhamon".

C. Cabeza de filósofo. Bronce, 243 a.C. |

E. Engranajes helicoidales dobles chinos, Xian, 50 d.C |
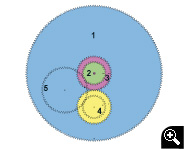
F. Engranaje diferencial del mecanismo de Antikythera. |
El engranaje diferencial de Antikythera
Se trata de un engranaje diferencial plano en el que, según se puede ver en el dibujo obtenemos el movimiento de la rueda (F) de engranajes azul [1] mediante la semisuma de las velocidades de los engranajes verde [2] y magenta [3]. El eje de las ruedas amarillas [4] va anclado a la rueda azul y la arrastra. La rueda transparente [5] es un mero transmisor de movimiento, también con su eje anclado a la rueda azul.
En nuestro mecanismo, si animamos el engranaje verde con el movimiento sidéreo lunar y la rueda magenta con el movimiento solar aparente, la rueda azul mostrará el movimiento sinódico lunar, es decir, las fases lunares.
En este caso, de relaciones de transmisión complicadas, el mecanismo diferencial es un método fácil de conseguir relaciones exactas.
En cuanto a los conocimientos necesarios para su diseño, en la Grecia de la época ya se conocían sobradamente los sistemas epicicloides de Apolonio de Pérgamo (262-190 a.C.) y de Hiparco de Nicea (190-120 a.C.) que se emplean en este mecanismo, ya que eran utilizados en los cálculos de las posiciones de los planetas, en ausencia de las leyes de Kepler, que se enunciarían 1.700 años más tarde.
El Proyecto Oficial de Investigación del Mecanismo de Antikythera
Los descubrimientos de Price resultaban demasiado "atrevidos" en los años 70 y no fueron admitidos inmediatamente. En las décadas de los '80 y '90 hubo nuevos avances de investigadores como Allan Bromley y Michael Wright, con un nuevo estudio de rayos X. Bromley murió en 2002, pero Wright continúa investigando y sospecha que el mecanismo de Antikythera también simula los movimientos de todos los planetas.
Pero el estudio más completo es el del Antikythera Mechanism Research Project (AMRP), una iniciativa oficial conjunta del Museo Arqueológico Nacional de Atenas y varias universidades griegas y del Reino Unido, que durante el otoño de 2005 llevó a cabo dos trabajos que han dado origen a los principales avances y que exponemos a continuación.
Dentro del propio Museo Arqueológico, se realizó un estudio con fotografía digital de las inscripciones superficiales, mediante un sistema de iluminación rasante, del Laboratorio Móvil de Sistemas de Medios de Hewlett-Packard (USA), que permitió ver cómodamente las inscripciones más accesibles.
Al mes siguiente llevó a cabo un estudio en rayos X, en tres dimensiones, mediante un equipo de X-Tek Systems (UK), un enorme tomógrafo portátil de 8 toneladas conocido como "BladeRunner CT", con software de Volume Graphics (D) y apoyo de la Universidad de Keele (UK). Obtuvo una resolución de 0,1mm en las 3 dimensiones.
Mediante esta tomografía se pudo tener acceso al detalle de todos los engranajes internos englobados en el cuerpo central, y se pudieron descifrar unos 3.000 caracteres grabados, de un total estimado de 15.000 que tiene el mecanismo.
Textos grabados descubiertos
Hay que aclarar que la existencia de las inscripciones ha sido fundamental para descifrar el mecanismo. Sin ellas, nunca se hubiera sospechado su posible uso, aplicación o procedencia, como veremos a continuación.
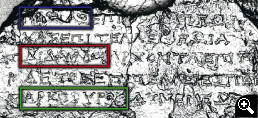
Las inscripciones mejor preservadas estaban en superficies que resultaron protegidas mientras el mecanismo estaba sumergido. Algunas de éstas resultaron expuestas más tarde, al fragmentarse, pero otras seguían ocultas, hasta que fueron reveladas por la tomografía en rayos X realizada en 2005. Ya en los primeros años de investigación se habían descubierto algunas referencias astronómicas (G), pero eran incompletas, lo que impedía interpretarlas en algún caso.
Datación por las inscripciones
Haralambos Kritzas dirigió el equipo del Museo Epigráfico de Atenas que dató el estilo de escritura, para lo que se basó en el estudio del texto (H) considerando detalles como los siguientes:
![]() , pi, tiene patas de distinta longitud: segunda mitad del siglo II a.C.
, pi, tiene patas de distinta longitud: segunda mitad del siglo II a.C.
![]() , sigma, los dos trazos no horizontales en ángulo: II a.C (final) ó I a.C.(inicio).
, sigma, los dos trazos no horizontales en ángulo: II a.C (final) ó I a.C.(inicio).
![]() , mu, tiene los dos trazos no verticales sino en ángulo: segunda mitad del II a.C. Sin embargo hay una M con los trazos verticales.
, mu, tiene los dos trazos no verticales sino en ángulo: segunda mitad del II a.C. Sin embargo hay una M con los trazos verticales.
![]() , upsilon, tiene la línea vertical corta: segunda mitad del siglo II a.C.
, upsilon, tiene la línea vertical corta: segunda mitad del siglo II a.C.
![]() , alpha, posterior a Alejandro Magno (300 a.C.).
, alpha, posterior a Alejandro Magno (300 a.C.).
![]() , zeta, tiene es como I con largas lineas horizontales: siglo II a.C.
, zeta, tiene es como I con largas lineas horizontales: siglo II a.C.
![]() , omega, no como
, omega, no como ![]() : siglo II a.C.
: siglo II a.C.
![]() , beta, círculos superior e inferior distintos: antigua.
, beta, círculos superior e inferior distintos: antigua.
![]() , omicron, muy pequeña: antigua
, omicron, muy pequeña: antigua
![]() , theta, tiene una línea corta en el centro y en un caso un punto: siglo II a.C.
, theta, tiene una línea corta en el centro y en un caso un punto: siglo II a.C.
![]() , phi, es como un arco: antigua.
, phi, es como un arco: antigua.
![]() , xi, linea central corta: antigua.
, xi, linea central corta: antigua.
Fruto de todas sus investigaciones, los especialistas en epigrafía concluyeron que la fecha más probable de fabricación del instrumento es entre 150-100 a.C.
La inscripción clave
Ya se había visto anteriormente en la inscripción de la parte trasera (I), la palabra ![]() (hélice o espiral), pero no se había podido relacionar con ninguna de las piezas, ni intuir a qué podía referirse.
(hélice o espiral), pero no se había podido relacionar con ninguna de las piezas, ni intuir a qué podía referirse.
Hubo que esperar a la tomografía de rayos X de 2005, cuando se descubrió que la frase continuaba: "subdivisiones 235".
Resulta que 235 meses tenía el calendario Metónico, que era un calendario lunisolar muy utilizado en Grecia en esa época y que se sospechaba era el representado en el dial trasero superior del mecanismo. Si en vez de un dial de círculos concéntricos, se trataba de un dial en espiral continua, éste marcaría consecutivamente las 235 divisiones del calendario Metónico completo. Y a partir de ahí se pudo deducir el uso de los demás componentes, como el dial trasero inferior, que también era en espiral, con un total de 223 divisiones, correspondientes a los meses que tiene un "Saros", o período de unos 18 años, a partir del cual se repiten los eclipses. La determinación de la ocurrencia de los eclipses era muy importante en la antigüedad. Se sabe que hay registros de hace muchos miles de años (tablillas babilónicas y chinas) de los eclipses ocurridos, por lo que, experimentalmente, se sabía con exactitud la medida de estos periodos.
Diseñar un dial en espiral tiene sus complicaciones, porque la aguja marcadora debía deslizar sobre la guía en espiral, pero sólo una de las divisiones de uno de los círculos sería la indicada. Y ésta es otra de las sorpresas del mecanismo, puesto que utilizaba para ello mecanismos de deslizaderas o agujas deslizantes y guías en espiral, como veremos más adelante. Al final de la espiral, el puntero debía volverse a cero manualmente.
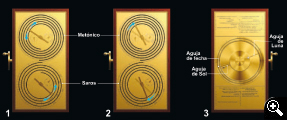
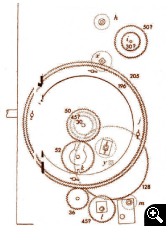
Los diales traseros (K)
- El Dial Metónico. Calendario lunisolar griego [1]. Estaba en la parte superior y tenía 47 divisiones por vuelta, con 5 vueltas, totalizando los 235 meses del ciclo Metónico de 19 años. Incorporaba días añadidos en los años considerados "bisiestos": 5 días de cada 19 años, dando un año bastante aproximado de 365,26 días. Los años eran de 12 meses (de 29 ó 30 días alternos) pero añadiendo un mes cada 2 ó 3 años, según una secuencia fija y exacta.
- El Multiplicador Calípico [2]. El calendario Metónico no era del todo exacto y para evitar la acumulación de errores se contaba con 4 ciclos metónicos, que hacían 4x19 años= 76 años, en los que se añadía 1 día cada 4 años, dando un año de 365,25 días (como el año egipcio y casi exacto al actual). Para ello, había una esfera pequeña dividida en cuatro cuadrantes, cuya aguja iba acumulando ciclos metónicos hasta un total de 4 (dentro del dial superior metónico, hay dos pequeños: el calípico a la izquierda y el olímpico a la derecha [5], que explicaremos más tarde).
- El Dial de Saros para predecir eclipses [3]. En su dial espiral contaba con 223 divisiones de meses sinódicos (el tiempo que tarda en producirse la misma fase lunar), equivalentes a 242 meses draconíticos (el tiempo en que tarda la Luna en volver al mismo nodo en su órbita) = 18 años, 11 días y 8 horas = 6.585,3 días, que es el período a partir del cual se repite el ciclo de eclipses: el Saros.
Además hay 239 meses anomalísticos completos en el Saros, (tiempo entre dos pasos de la Luna por su perigeo) por lo que están marcados en su lugar, los eclipses que son totales y parciales. Hay 239-223=16 ciclos en un Saros; por eso está dividido en 4 vueltas y en cada una hay 4 ciclos completos lunares (coincide fase, tamaño y tipo de eclipse)
- El Multiplicador Exeligmos [4]. El ciclo de Saros es lo que tarda en repetirse un mismo eclipse, pero no sobre el mismo punto de la Tierra sino a unos 120º sobre su superficie. Cada 3 ciclos Saros = 3 x 18 años = 54 años y 34 días ![]() 19.756 días sí se repite casi exactamente el eclipse sobre el mismo punto de la Tierra. Para eso se construyó un acumulador de 3 Saros, llamado Exeligmos, que aparece en el interior de la esfera inferior, a la derecha del centro.
19.756 días sí se repite casi exactamente el eclipse sobre el mismo punto de la Tierra. Para eso se construyó un acumulador de 3 Saros, llamado Exeligmos, que aparece en el interior de la esfera inferior, a la derecha del centro.
Con éstos y el dial frontal, se podían predecir los eclipses de Sol y Luna, con hora, día, mes y año.
La interpretación de los diales traseros
En el dial de Saros (inferior) hay inscripciones en sólo algunos de los 223 meses (en los que se produce algún eclipse), con 4-10 caracteres que definen las características del eclipse o eclipses.
Veamos un ejemplo de uno de los meses en los que aparece la inscripción:
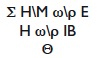
El significado es el siguiente:
![]() =
= ![]() = SELENE (eclipse lunar).
= SELENE (eclipse lunar).
H = ![]() = ELIOS (eclipse solar).
= ELIOS (eclipse solar).
H\M = ![]() = EMERAS (del día).
= EMERAS (del día).
N\Y= ![]() = NICTOS (de la noche).
= NICTOS (de la noche).
![]() E =
E = ![]() E = hora E.
E = hora E.
![]() = letra de no de orden del eclipses.
= letra de no de orden del eclipses.
Así pues, en este mes del Saros se producirían dos eclipses, uno de Luna, durante el día, a la hora E y otro de Sol a la hora IB.
En el dial Metónico (superior) aparecen los nombres de cada mes en cada casilla de las 235 y en su interior, además del pequeño dial calípico hay otro dial que se explica a continuación.
El dial olímpico
Entre los textos desvelados en 2005 por la tomografía aparecieron referencias a los Juegos Olímpicos Panhelénicos principales, recogidos en un dial. Éste, dividido en cuatro partes, acumulaba cuatro años y marcaba los juegos olímpicos que correspondía celebrar ese año, según una rotación cíclica.
- El primer año: ![]() ,
, ![]() A = año 1:
ISTMIA (Corinto, primavera);
A = año 1:
ISTMIA (Corinto, primavera); ![]() (OLIMPIA, verano).
(OLIMPIA, verano).
- El segundo: LB NEMEA, NAA = año 2: NEMEA (verano), NAA (Juegos menores de Dodona)
- El tercero: ![]() = año 3: ISTMIA (Corinto, primavera) y PITIA (Delphos, fin verano)
= año 3: ISTMIA (Corinto, primavera) y PITIA (Delphos, fin verano)
- El cuarto: ![]() = año 4: NEMEA y texto sin descifrar
= año 4: NEMEA y texto sin descifrar
La fecha de los Juegos Olímpicos (en Olimpia), los más importantes, se celebraban cada cuatro años, comenzando en la luna llena más próxima al solsticio de verano, que calculaban mediante el mecanismo principal del aparato.
Diales frontales
En el dial frontal había, como puede verse en la radiografía de la pieza original (M), dos diales concéntricos, perfectamente graduados y que podían deslizar uno sobre otro. El exterior [1] era el dial del año egipcio (Sótico), que tenía 365 días, divididos en 12 meses de 30 días y un suplemento de 5 días añadidos. Esta escala era móvil y podía irse girando para añadir un día cada año bisiesto. Para ello se giraba y fijaba con un pasador que encajaba en los 365 taladros que había debajo de la escala.
El dial zodiacal [2], más interior, representaba la eclíptica, con su escala dividida en los 12 signos de constelaciones zodiacales y en 360 grados.
Sobre ellos, señalaban las distintas agujas o punteros coaxiales (O), como: el puntero de posición de la Luna [1], el simulador rotatorio de fases de la Luna [2], el puntero de posición del Sol [3] y el puntero o aguja de día del año [4]. Se ha propuesto que también se mostraban las posiciones de los planetas, pero aún no está demostrado.
Además, en la placa fija frontal estaba grabado el "Parapegma" o almanaque: una tabla con ortos y ocasos de estrellas de referencia y constelaciones (Pléyades, Hyades, Vega, Arcturo, Altair, Geminis).
El cálculo del próximo eclipse
Mediante este dial frontal y los traseros se pueden predecir los eclipses próximos de esta forma (P):
1. Primero, se gira la manivela para poner el mes y año de la fecha actuales en el dial Metónico (arriba). El puntero del Saros se moverá también con el paso del tiempo.
2. Luego se gira la manivela avanzando el tiempo, hasta que el puntero del Saros señale una inscripción de eclipse. Esa inscripción indicará si se trata de un eclipse lunar o solar y el mes y la hora, pero no el día del eclipse.
3. En el dial frontal, se ajusta con la manivela, muy suavemente, hasta que los punteros del Sol y la Luna estén alineados (eclipse solar) u opuestos a 180º (eclipse lunar) El puntero de día señala en la escala del calendario egipcio el día en que se producirá el eclipse.
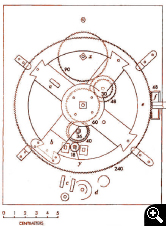
Cadena cinemática y montaje
29 de los 30 engranajes existentes eran para el cálculo de posiciones de Sol y Luna y fases de ésta, incluso las anomalías de ambos, y para el cálculo de eclipses (Q).
Mediante la tomografía de 2005 se ha podido determinar el número de dientes de cada uno de los 30 engranajes y comparar la exactitud con que reproducían los ciclos celestes (meses, años, eclipses) con los reales, comprobando que su exactitud era de 1/40.000.
En la Figura (R), se representan las diversas cadenas cinemáticas con flechas de diferentes colores, todas ellas partiendo del engranaje principal que se accionaba mediante una manivela y un engranaje a 90º con él. Una vuelta de esta rueda coincide con el paso de un año y se marcaba sobre el dial de año egipcio.
En azul, la cadena metónica, en la parte superior, que acaba bifurcándose para la representación del dial de la hélice principal (A azul), de su multiplicador calípico (E) y del acumulador de 4 años olímpico (D).
En amarillo, compartiendo las primeras ruedas dentadas de la cadena anterior y luego cruzando al lado inferior a través de la gran rueda de la plataforma lunar (A naranja), para bifurcarse al final en el puntero de Saros (A amarilla) y su multiplicador exeligmos (B).
En naranja, la complicada cadena del movimiento lunar, partiendo de la rueda principal por una vía propia, hasta la plataforma de movimiento lunar (A naranja) y las ruedas epicíclicas iguales de simulación de anomalía lunar (B). Nótense el pasador y la ranura de las ruedas para el arrastre excéntrico. El movimiento retornaba a través de la otra pareja de ruedas mediante un eje coaxial interior al de llegada del movimiento. Luego se transmitía, también mediante un eje coaxial con el de la rueda principal para llegar a un engranaje cónico (C) que hacía girar una esfera pintada la mitad en blanco y la mitad en negro (D) que simulaba la fase lunar y un puntero que marcaba la edad lunar sobre el dial frontal.
El simulador de fases lunares
Dentro de ese conjunto encontramos mecanismos avanzados, como los engranajes cónicos para el simulador de fases lunares, que es en sí mismo un gran desarrollo y que sólo volvemos a encontrar en algún reloj astronómico del siglo XVII. Para entender su funcionamiento ver la reconstrucción moderna presentada en la Figura (S).
El mecanismo avanzado de arrastre excéntrico para la Luna y de simulación de fases lunares
T. Esquema de funcionamiento del sistema de anomalía lunar. En el mecanismo, las ruedas 1, 2, 3 y 4 son todas de 50 dientes e iguales. En la figura se han hecho diferentes para facilitar su comprensión. El centro de la rueda del pivote [2] está desplazado respecto al centro de la rueda de la ranura [3].
V. Engranaje r1, fragmento D
U. Esquema de funcionamiento del puntero excéntrico solar.
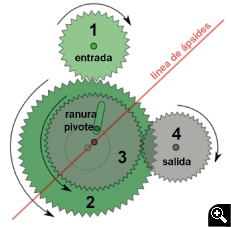
Uno de los misterios que más tardaron en descifrarse fue la existencia de cuatro ruedas iguales, de 50 dientes, que pertenecían a la Luna y que no parecían servir de nada (relación de transmisión= 1).
Wright, uno de los investigadores, había descubierto un pivote en una de las ruedas epicicloides, que encajaba en una ranura de otra que estaba inmediatamente debajo. Aún así, el mecanismo no tuvo sentido hasta que se comprobó que los ejes de ambas ruedas estaba desplazados ligeramente (T).
Ese arrastre excéntrico desplazado del eje era un simulador de anomalía lunar (diferencia entre la posición real de la Luna en su órbita elíptica y su posición teórica que tendría en una orbita circular ideal y con movimiento uniforme) según la teoría de epiciclos de Hiparco, y es el mismo sistema que se utiliza en los planetarios opto-mecánicos actuales para poder aproximar el movimiento de la Luna y planetas a su movimiento real, mediante las leyes de Kepler.
Otro problema era el del movimiento de los ápsides de la órbita lunar: cada 8,85 años el perigeo (punto más cercano de su órbita elíptica) da un giro completo alrededor de la Tierra. La cuidada relación de engranajes que movía el sistema cicloide también hacía girar la línea de ápsides lentamente, al mismo tiempo.
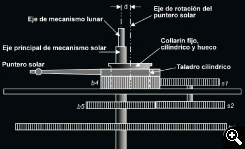
El sistema de simulación del Sol
El movimiento aparente del Sol presenta también una anomalía debido a que la órbita de la Tierra tiene una pequeña excentricidad. La anomalía solar producida por esa excentricidad se conseguía simular desplazando un poco el eje respecto al centro de la escala, para conseguir velocidades variables en la proporción adecuada. Como la escala es la misma que utiliza el calendario sótico o egipcio, se desplazaba el eje del puntero solar. Como el eje es coaxial con los demás, se construía un collarín hueco desplazado, al que se llevaba el movimiento a través de engranajes laterales (U).
Este sistema de simulación es similar también al empleado en los planetarios mecánicos actuales.
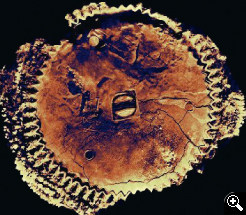
El engranaje no 30
Hay otro engranaje (llamado r1, de 63 dientes en el fragmento D) (V) del que no se conoce la función. Se sospecha que podía mover un sistema epicicloide de planetas. Hay indicios de la existencia de esos epiciclos, al menos para los casos de Mercurio y Venus, puesto que hay inscripciones como: "Hermes, Afrodita, estacionario", que pueden referirse a los momentos en que Mercurio y Venus frenan su avance y paran su movimiento aparente geocéntrico, antes de iniciar el movimiento inverso en los bucles que describen en el cielo.
Si el mecanismo resolvía Mercurio y Venus, podía resolver también Marte Júpiter y Saturno. Según Wright, otro de los investigadores, hay indicios de epiciclos perdidos para los cinco planetas. También se ha apuntado la posibilidad de que existiera una aguja adicional en el dial frontal para mostrar la edad de la Luna, puesto que el simulador de fases es útil para comprobar su aspecto general, pero no es muy exacto para la determinación del día del mes lunar, por prestarse a una apreciación subjetiva.
Aspecto general
El tamaño total del mecanismo era de 33cm x 18cm x 10cm, aunque este último dato es menos seguro, debido a que el mecanismo estaba aplastado bajo las tablas del barco (W).
Las instrucciones de uso estaban en las dos tapas internas, "parapegma" y en la placa trasera.
¿Quién pudo construirlo?
La fecha de la construcción del mecanismo es fundamental para saber quién pudo hacerlo. Entre los objetos hallados en el barco hundido, los más modernos son las monedas de Pérgamo acuñadas entre el 86 y 67 a.C. y de Éfeso, acuñadas entre el 70 y 60 a.C. Puesto que no aparecen monedas más modernas, es de suponer que el naufragio ocurrió probablemente hacia el año 60 a.C. Pero el barco (con maderamen del 200 a.C.), parecía transportar un botín de guerra, probablemente de Pérgamo como consecuencia de la 1ª guerra contra Mitrídates (84 a.C.), que contenía elementos más antiguos, como las estatuas de bronce que datan de los siglos III y IV, por lo que nuestro mecanismo podría ser más antiguo.

W. Vista frontal de un modelo para una exposición en un museo de Nueva York en 2007. Se puede ver parte del manual con referencias astronómicas, geográficas y técnicas en la parte de las cubiertas o puertas. Fuente: Evans 2010.
X. Reparación, pieza b añadida. Imagen original del mecanismo tal como consignaba Derek de Solla Price en el artículo de Scientific American de 1959
Y. Cajeado k en la rueda de 52 dientes para insertar nuevo diente. Del artículo original de Scientific American de 1959.
Debido a que la fecha que señalaba era el año 85 a.C., se creyó en un principio que podía haberse construido pocos años antes de esa fecha, pero todos los indicios, especialmente los textos grabados, apuntan a que se construyó hacia los años 150-100 a.C.
Además, el mecanismo presenta dos reparaciones: una sobre una unión en "cola de milano" (que ya se usaba en la época) (X, pieza b), lo que implica un cierto uso anterior al naufragio.
Y otra reparación en uno de los dientes, que había sido retirado para insertar el nuevo en un cajeado hecho en la rueda (Y, pieza k). Esto que supone que el mecanismo habría sido usado durante algún tiempo y sería más antiguo que el naufragio, encajando en el periodo 150-100 a.C.
En cuanto a su procedencia, por el tipo de calendario (metónico) y el nombre de los meses, sabemos que era Corintio: bien construido en Corinto, antes de su destrucción por los romanos en el 146 a.C., o en las colonias corintias del norte de Grecia, o más probablemente en Sicilia.
Nuestro primer sospechoso es Arquímedes, que fue inventor y construyó muchos mecanismos con engranajes triangulares, e incluso investigaciones recientes proponen que inventó un engranaje de perfil curvo de mejor rendimiento.
Arquímedes murió en Sicilia en 212 a.C, defendiendo Siracusa contra el ataque de los romanos. Según las crónicas, el conquistador de esta ciudad, el general romano Marco Claudio Marcelo, como parte del botín, se llevó a Roma dos instrumentos astronómicos hechos por Arquímedes.
Uno, fue la única pieza del botín que se quedó. El otro, se colocó en el templo de Vesta. Ambos reproducían los movimientos del Sol, la Luna, los "errantes", y predecían los eclipses. Se ha perdido el libro que Arquímedes escribió sobre métodos para su construcción, pero hay referencias de él y de su contenido: Pappus de Alejandría (IV d.C.) habla de un libro de Arquímedes sobre la "construcción de las esferas".
Pero estos mecanismos fueron construidos un siglo antes que nuestro mecanismo de Antikythera y fueron vistos en Roma a lo largo de los siglos siguientes por varios cronistas que dejaron su descripción o su existencia por escrito: una referencia importante es un texto de Cicerón (De Re Publica 1.21-22) Dice que Marco Sulpicio Galo vio en Roma, en el año166 a.C. la "esfera de Arquímedes" que mostraba los movimientos de un globo celeste, sobre el que se reproducían los movimientos del Sol, la Luna y los planetas, con sus velocidades propias diferentes y que era capaz de reproducir eclipses. Ovidio la vio en el siglo I d.C. y la describe brevemente en los FASTOS VI, 277; Sextus Empiricus (II d.C.) la vio y describe como se mueve; Lactancio (IV d.C.) la describe; Claudio Claudianus (400 d.C.) tiene un poema sobre la esfera de Arquímedes; Proclo (V d.C.) comentario en el primer libro de Euclides, Elementos de Geometría.
Además, Arquímedes no tuvo en cuenta la anomalía lunar, que es calculada por Hiparco varias décadas más tarde, ni la reprodujo en sus máquinas. Sin embargo, uno de sus mecanismos pudo ser el original, que fuera copiado, enviado a otros lugares y mejorado posteriormente.
Otra línea de investigación, reconstruyendo la ruta seguida por el barco naufragado, con ayuda de los restos hallados en las exploraciones submarinas primitivas y otras posteriores de Cousteau en 1953 y 1975-1978, dedujo que debía proceder de la Grecia oriental: Pérgamo, Kos o, más probablemente, de Rodas.
Ese origen encajaría con otro texto de Cicerón que habla de algo similar al mecanismo de Antikythera, construido por el filósofo estoico griego Posidonio de Rodas: El instrumento "construido recientemente por mi amigo Poseidonios, con cada revolución reproduce los movimientos del Sol, la Luna y los cinco planetas". (De Natura Deorum, ii, 34.)
Posidonio (c. 135 a. C.-51 a. C.) fue un político, astrónomo, geógrafo, viajero, historiador y filósofo, nativo de Apamea, Siria. Muy famoso en su tiempo, llegó a ser embajador en Roma, por lo que pudo tener acceso al ejemplar de Arquímedes.
Dirigió una prestigiosa escuela astronómica, que había fundado Hiparco en la isla de Rodas. Han sobrevivido algunos fragmentos de sus trabajos y se cree que el tratado del astrónomo griego Cleómedes sobre los movimientos circulares de los cuerpos celestiales en parte fue copiado de una obra de Posidonio.
Posidonio calculó la distancia al Sol y los tamaños de la Tierra, de la Luna del Sol en el año 90 a.C., con resultados mucho mejores que los de Aristarco de Samos siglo y medio antes.
Cicerón relata haber visto el instrumento con sus propios ojos en esta ocasión, en su libro, en el 45 a.C.
Lamentablemente, nuestro mecanismo de Antikythera debía estar ya construido hacía décadas y ya estaba bajo el mar cuando Posidonio construyó su máquina; lo más probable es que ésta fuera una copia o variante de otro "mecanismo" anterior (posiblemente de Hiparco, de quien pudo ser discípulo).
Ninguno de los mencionados en las crónicas era pues el mecanismo de Antikythera, pero tiene sentido suponer que hubiera varios mecanismos construidos en distintas partes del mundo, derivados o copiados unos de otros y que el mecanismo se fuera perfeccionando con el tiempo. De todos ellos nos ha llegado sólo uno y gracias a muchas coincidencias afortunadas que lo conservaron bajo el mar y pudo ser encontrado 20 siglos más tarde. A este respecto hay que recordar que el bronce era muy valioso y que muchas veces eran refundidas las piezas, para obtener otras.
Hay un intento serio de relacionar el mecanismo con el propio Hiparco (190-120 a.C), uno de los sabios antiguos que inventó la trigonometría e hizo contribuciones muy importantes a la astronomía. Además de vivir justo en la época de su construcción, Hiparco tenía en cuenta la anomalía lunar y elaboró un modelo de epiciclo para el movimiento de la Luna y del Sol. También fundó la Escuela de Rodas que desarrolló enormemente la astronomía y posiblemente construyera simuladores mejorados. Así, el origen del mecanismo coincidiría con la Isla de Rodas. Se especula que Hiparco, o alguno de sus discípulos inmediatos, pudiera haber tomado como modelo el mecanismo de Arquímedes, copiando su calendario y el nombre de los meses, pero introduciendo en él sus epiciclos para el cálculo de la Luna y el Sol.
Conclusión
Durante mucho tiempo se estuvo dudando del origen tan antiguo del mecanismo porque se pensaba que la tecnología griega no podía haber sido tan avanzada en el siglo II a.C. En cuanto a esto, ha habido hallazgos recientes que han ayudado a "redescubrir" el gran nivel científico y tecnológico de civilizaciones antiguas como la babilonia, china, egipcia o griega. Nos han llegado sus descubrimientos a veces por puro azar, pero hemos podido interpretarlos y descifrar su funcionamiento gracias a que estaban muy bien documentados: llevaban grabadas las instrucciones en sus propias piezas. Los antiguos griegos tenían el conocimiento y las técnicas necesarias para construir aparatos tan complejos y precisos como el mecanismo de Antikythera. Sorprendentemente, esos conocimientos desaparecieron y no volvieron a reaparecer en nuestro mundo occidental hasta el Renacimiento. Posiblemente, muchos otros se perdieron para siempre... ¿Qué motivos hubo para que tuviera lugar ese gran paréntesis en la cultura humana?.