
Home > La manzana de Newton vista por Einstein

Autor: Luis García Pascual

Luis García Pascual Doctor Ingeniero Electromecánico del ICAI (Promoción 1957). Diplomado en Organización Industrial. Profesor Emérito de la ETSI ICAI (UPC).

Yolanda González-Arechavala Doctora Ingeniero Industrial del ICAI por la Universidad Pontificia Comillas y Licenciada en Informática por la Universidad del País Vasco. Actualmente, es Profesora del Departamento de Sistemas Informáticos e Investigadora del Instituto de Investigación Tecnológica de la ETSI ICAI. Sus áreas de investigación están centradas en el análisis de sistemas de seguridad ferroviarios y en el análisis de ciclo de vida y uso de la biomasa como fuente de energía sostenible.

Carlos Martín-Sastre Ingeniero Agrónomo (UPM) y Máster en Investigación en Modelado de Sistemas en Ingeniería por la Universidad Pontificia Comillas. Actualmente es Investigador en Formación del Instituto de Investigación Tecnológica de la ETSI ICAI. Sus áreas de investigación están centradas en el análisis de ciclo de vida y el uso de la biomasa como fuente de energía sostenible.
Palabras clave: Atracción gravitatoria, Relatividad especial, Relatividad general, Espacio-tiempo, Tensor métrico, Curvatura del espacio-tiempo, Líneas geodésicas.
Key words: Gravitational attraction, Especial relativity, General relativity, Space-time, Metric tensor, Space-time curvature, Geodesic lines.
Resumen: En este artículo se recuerdan los efectos de la gravedad sugeridos por Newton partiendo del valor de la fuerza de atracción entre dos masas cualesquiera y, como quiera que los mismos efectos fueron refrendados posteriormente por la teoría de los campos electromagnéticos, la interpretación newtoniana de la gravedad se ha venido utilizando, sin ninguna reserva, durante más de doscientos años. No obstante, en esta interpretación se admitía que la acción de la gravedad se propaga instantáneamente a través del espacio que separa entre sí las dos masas protagonistas de la fuerza de atracción entre ellas. La Teoría de la Relatividad puso de manifiesto que la velocidad de aquella propagación no puede superar la velocidad de la luz (300.000 km/s), afirmación que dio origen a una auténtica crisis científica. Crisis que fue superada gracias a la clarividencia de Einstein y a las aportaciones de eminentes matemáticos (sobre todo Gauss y Riamann) del siglo XIX. Inquietar e ilusionar al lector, frente a la aparentemente extraña interpretación einsteiniana de la gravedad como curvatura del espacio-tiempo ocasionada por la presencia de masas en él, es el objetivo pretendido en este artículo.
Abstract: In this article, we review the effects of gravity indicated by Newton, starting from the value of the pulling force between any two bodies. As these effects were confirmed by the electromagnetic fields theory, the newtonian interpretation of gravity has been used, without any limitation, for more than two hundred years. However, this interpretation admitted that the gravity action is instantly propagated throughout the distance between two bodies that are attracted. The relativity theory highlighted that the speed of such propagation can not be higher that the speed of light (300.000 km/s), which led to a true crisis in the scientific area. This crisis was overcame due to the astuteness of Einstein and the inputs of great 19th century matemathicians (specially Gauss and Riamann). The goal of this article is to rattle and encourage the reader about the apparently bizarre Einstein´s interpretation of the gravity as a space-time curvature, originated by the presence of any mass in it.
Para Newton el mundo era una gigantesca maquinaria de relojería, donde el hombre todo lo podía calcular y todo lo podía medir. Para Einstein, en cambio, es una inmensa distribución de materia a lo largo del espacio y con el transcurrir del tiempo, donde el hombre puede soñar (John Weeler -1911-2008).
Introducción
Sir Isaac Newton (1643-1727) ocupa, por muchísimas razones, un puesto muy destacado en la Historia de la Ciencia, aunque, desde la perspectiva de este artículo, únicamente mencionaremos los cuatro motivos siguientes:
- - Haber puesto de manifiesto que la caída vertical y hacia el suelo de la manzana era, simplemente, consecuencia de la atracción recíproca que existía entre la Tierra y la manzana.
- - Esta atracción daba origen a una fuerza de la Tierra sobre la manzana y de ésta sobre aquella, fuerza cuyo valor venía determinado por la expresión:
- - Dejar constancia de que el movimiento de la manzana hacia el centro de la Tierra no era uniforme sino que en este movimiento la velocidad cambiaba según el propio Newton había establecido en su segundo principio, aparecido en 1687 en su famosa obra Philosophiae Naturalis Principia Mathematica. En este principio Newton afirmaba "mutationem motus proportionalem esse vi motrici impressae et fieri secundum lineam rectam qua vis illa imprimitur"; es decir "el cambio de movimiento de un cuerpo es proporcional a la fuerza exterior que se le aplique y ocurre según la línea recta en la cual aquella fuerza se aplique".
- - Haber descubierto que la Tierra gira alrededor del Sol por el mismo efecto físico por el que caen las manzanas; porque el Sol atrae a la Tierra y no la deja escapar.
en la que:
G es la constante de gravitación universal (6,67259. 10-11kg-1m3s-2).
M la masa de la Tierra.
m la masa de la manzana.
r la distancia entre ellas.
No obstante, Newton ponía cierta sordina ante sus aportaciones a la Filosofía de la Naturaleza cuando en una de sus cartas manifestaba que "la gravedad sea innata, inherente y esencial para la materia de tal manera que un cuerpo pueda actuar sobre otro, a distancia, a través del vacío y sin la mediación de ninguna otra cosa por la cual y a través de la cual se pueda transmitir la fuerza entre estos cuerpos (del uno al otro y del otro al uno), es algo completamente absurdo. Debe haber un agente que cause la gravedad actuando constantemente de acuerdo con ciertas leyes que dejo a la consideración de mis lectores".
Por otra parte, también es interesante recordar que el hecho de que la interpretación newtoniana de la gravedad describiera con precisión matemática sus "efectos", aunque omitiera establecer sus "causas", ya debía colmar las aspiraciones de Newton; puesto que, en alguna ocasión, afirmó "yo no hago hipótesis, constato hechos".
A pesar de estas limitaciones, en la propuesta newtoniana sobre la gravedad, la Ciencia se acomodó con tal entusiasmo y tan fuertemente a ella que, durante más de 200 años, nadie se atrevió a afrontar el reto lanzado por Newton e inte ntar descubrir el verdadero "agente motivante" de sus efectos, efectos que, con tanta precisión, él había puesto de manifiesto. Albert Einstein (1879-1955), a pesar de su intuición para percibir las entrañas ocultas que rigen el comportamiento de la Naturaleza y de su facilidad para razonarlas, necesitó diez años de trabajo (de 1905 a 1915) y el consejo y la ayuda de su compañero de clase Grossman (1878-1936) para estudiar y aplicar los hallazgos obtenidos por la pléyade de los insignes matemáticos alemanes de los siglos XVIII y XIX –sobre todo por Gauss (1777-1855) y por Riemann (1826-1866). La genialidad de Einstein y la profundidad de las sugerencias de Gauss y de Riemann sirvieron para conocer y explicar mejor la gravedad.
Si Newton supo cuantificar los "efectos" de la gravedad pensando en la caída de una manzana, Einstein mejoró su comprensión razonando también sobre la supuesta caída de un posible despistado que, sobrepasando los límites de la terraza de un edificio, situado frente a la ventana de su mesa en la oficina de patentes donde trabajaba en Berna, pudiera precipitarse al vacío y cayera hacia el suelo (como la manzana) con idéntico movimiento, aunque percibido por Einstein con diferente mentalidad a la preconizada por Newton. Si Newton vio en la caída de la manzana una fuerza, Einstein en la caída del despistado consideró sobre todo una aceleración en el movimiento relativo entre el desgraciado que se desplomaba en el vacío y él que lo contemplaba sentado en su silla.
Propuesta de Newton
Newton, anclado en el determinismo clásico, pensaba que el valor tanto de cualquier intervalo de espacio como de cualquier intervalo de tiempo, ambos medidos con sus propios aparatos de medida por distintos observadores, eran idénticos aunque entre los distintos observadores hubiera movimiento relativo y, en consecuencia, tanto el espacio recorrido por la manzana como el tiempo empleado en recorrerlo eran iguales en el "sentir" de Newton, sentado al pie del manzano, y en el "pensar" de otro posible observador moviéndose solidariamente con la manzana. Bajo este supuesto, Newton más o menos razonaría de la siguiente manera:
- - Existe un espacio plano y tridimensional de Euclides X Y Z en el que cae la manzana y en el que también me encuentro yo. A la vez dispongo de un reloj que registra el tiempo T y de un metro que constata el espacio Z medidos desde que la manzana se suelte del árbol hasta que llegue al suelo.
- - La masa M de la Tierra ejerce una fuerza
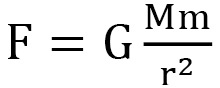 sobre cualquier masa m que pudiera encont rarse en cualquier punto determinado de dicho espacio X Y Z y, por lo tanto, también sobre la manzana.
sobre cualquier masa m que pudiera encont rarse en cualquier punto determinado de dicho espacio X Y Z y, por lo tanto, también sobre la manzana. - - El movimiento, que percibo en la manzana al caer, es variable con el tiempo, y este cambio podría cuantificarse como el producto de su masa m por la modificación de su velocidad VZ según el eje vertical. Por otra parte, la razón por la que aparece este cambio se debe al producto de la fuerza vertical aplicada a la manzana por el tiempo durante el que dicha fuerza esté actuando. Es decir:
- - Por un lado, la masa de la manzana es su propia masa bajo cualquier circunstancia y, por lo tanto, independiente de la velocidad que vaya teniendo en los distintos puntos de su caída y, por otro, la fuerza FZ aplicada es prácticamente constante en todos los momentos T de su recorrido (puesto que, en la ecuación [1], G, M y m lo son y r varía poquísimo). Por lo tanto, la ecuación [2] puede escribirse:
- - Como los incrementos de velocidad y de tiempo tienen lugar en cada instante, siguiendo las ideas sobre cálculo infinitesimal que, simultáneamente, preconizaban Newton y su contemporáneo y adversario científico Leibniz (1646-1716), probablemente en su cuaderno de notas, Newton escribiría lo que, en la notación matemática de hoy, expresaríamos de la forma:
y de aquí inmediatamente deduciría:
dividiendo ambos miembros por m, obtendría por fin la aceleración con la que descienden tanto la manzana de Newton como el despistado en el que, más de doscientos años después, pensara Einstein. El valor de esta aceleración será:
Un siglo más tarde, la propuesta de Newton se encuadró en un nuevo marco de comprensión gracias al concepto de campo que, en el estudio del electromagnetismo, introdujo con tanto éxito Faraday (1791-1867). Efectivamente, considerando que la masa M de la Tierra genera en todo el espacio X, Y, Z que la rodea un campo con potencial Φ de atracción hacia su centro de valor ![]() , que como consecuencia de dicho campo aparece una fuerza de atracción sobre la unidad de masa que vale:
, que como consecuencia de dicho campo aparece una fuerza de atracción sobre la unidad de masa que vale:
y que, si en [4] se sustituye Φ por su valor teniendo en cuenta que la atracción de la Tierra sobre la masa de la manzana tiene la misma dirección pero sentido contrario a Z, la expresión resultante coincide con la ecuación [3] propuesta con más de 100 años de antelación por Newton.
Respuesta de Einstein
Einstein encontraba en los razonamientos de Newton ciertos supuestos no asumibles. Entre ellos citemos:
- - A partir de los ensayos de Michelson y Morley (realizados en 1887), para dos observadores con movimiento relativo entre ellos (uno podría ser el propio Newton y otro el supuesto observador solidario a la manzana) ni se conserva el valor del espacio recorrido por la manzana al caer desde el árbol al suelo, ni es igual el tiempo empleado en recorrerlo, ni la masa de la manzana puede considerarse independiente de su velocidad. Lo único que no cambia de valor, para los dos observadores, es la velocidad de la luz
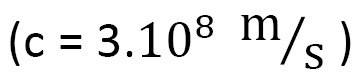 .
. - - Por otro lado, pensemos también que en el valor, supuesto por Newton para la aceleración con que caía la manzana, interviene la distancia r entre el centro de la Tierra y el punto donde aquella se encuentre; pero ¿quién mide esta distancia, Newton ó el observador que se desplaza con la manzana?
- - En las expresiones propuestas en la interpretación newtoniana de la gravedad no aparece para nada el tiempo, lo que implica que la acción de la fuerza, causante de la aceleración en el movimiento de la manzana, se aplica instantáneamente y ello viola frontalmente el precepto relativista de que ninguna señal puede viajar más deprisa que la luz.
En su intento por superar todas estas incoherencias, Einstein analizó, con su proverbial sagacidad, algún detalle que, siendo común en el sentir pro pio del supuesto observador solidario a la manzana y en la sensación del despistado individuo cayendo desde la terraza, pudiera orientar hacia una interpretación nueva de la gravedad libre de las incoherencias de la interpretación newtoniana. En este análisis nuestro genio se percató de que:
- - Antes de iniciarse la caída, ambos estaban sometidos a una fuerza vertical y hacia arriba (a la manzana se la aplicaba el rabito que la sujetaba al árbol y al despistado se la transmitía el suelo de la terraza sobre el que se apoyaban sus pies).
- - Una vez iniciada la caída, para los dos había desaparecido aquella fuerza y ambos bajaban con la misma aceleración, como ya había comprobado Galileo (1564-1642) al constatar que una bola de madera y otra bola de hierro, a pesar de su diferencia de densidad, caen de la misma manera por la acción de la gravedad g. En los dos casos había desaparecido la fuerza y, en su lugar, había hecho acto de presencia la misma aceleración g. Ello sugirió a Einstein su Principio de Equivalencia (the happiest thought of my life –llegó a decir). De la misma manera que, si un observador estuviera dentro de un ascensor, aislado completamente del exterior y el ascensor cayera con la aceleración g (por haberse roto el cable del que pendía), nuestro ascensorista, teniendo como referencia los fenómenos detectables en el interior de las paredes del ascensor, no sería capaz de distinguir si, instantáneamente, había desaparecido la gravedad o si se había roto el cable que soportaba el ascensor.
Einstein cohonestó la presencia de la fuerza antes de la caída y el concurso de la aceleración a lo largo del tiempo en que ocurría la misma, explicitando a qué o a quién se aplicaba la fuerza en el primer caso y entre qué existía aceleración en el segundo. Para ello razonó de la siguiente forma:
- - Los sucesos (Newton observando la caída de la manzana y ésta cayendo en el aire) obedecen a relaciones matemáticas que pueden representarse en una nueva estructura de superficies curvas en el sistema cuadrimensional definido por tres coordenadas espaciales y el tiempo. Como ya estableció Minkowski (1864-1909) es este espacio-tiempo la estructura en la que pueden estudiarse todos los eventos que tienen lugar en la Naturaleza.
- - Para analizar el movimiento de la manzana, el del despistado o el del ascensor, resulta necesario pensar en dos sistemas de referencia de espacio-tiempo:
- - El espacio-tiempo X, Y, Z, cT asociado al observador O que puede ser Newton con sus pies en el suelo o Einstein sentado en su silla viendo como cae la manzana con la aceleración g.
- - El espacio-tiempo x, y, z ct correspondiente al observador o (anclado a la manzana, unido al despistado o sentado en el ascensor) y que desciende libre de fuerzas aplicadas con una aceleración g respecto al espacio-tiempo anterior. Para este observador o (concretándonos al caso de la manzana) ésta no se mueve pero, en cambio, el árbol (y toda la Tierra con él) "sube" con cierta aceleración.
En consecuencia, para Einstein era necesario estudiar el proceso de la caída de la manzana en ambos sistemas de referencia bajo las siguientes circunstancias:
- - Para Newton como observador O, descendía la manzana en su espacio-tiempo X, Y, Z, cT la cantidad δZ y empleaba en este descenso un tiempo δcT.
- - Para el observador o, solidario a la manzana, el árbol subía, en su espacio x, y, z, ct con cierta aceleración (distinta de g, aunque para nuestra pretensión en este artículo no es necesario calcular) un desplazamiento δz y empleaba en dicho desplazamiento un tiempo δct, sabiendo, según la Teoría de la Relatividad Especial, que:
y de la misma forma:
Si, en lugar de estudiar el desplazamiento δZ ≠ δz en el tiempo δcT ≠ δct, pensáramos en un desplazamiento elemental durante un tiempo también elemental se tendría:
y:
Para encontrar la relación entre la formulación matemática del mismo fenómeno desde uno y otro sistema de referencia tanto para dcT y dct como para dZ y dz, Einstein sabía, por su Teoría de la Relatividad Especial, que, en cualquiera de los dos sistemas de referencia, no podían establecerse relaciones matemáticas de espacios por un lado y de tiempos por otro sino que, entre dos eventos correspondientes a dos puntos y en dos instantes infinitamente próximos, en cada uno de los dos espacios temporales (el x, y, z, ct para el observador o y el X, Y, Z, cT para el observador O), era necesario trabajar con los correspondientes intervalos en el espacio de cuatro dimensiones, siendo para o el cuadrado del intervalo:
e, igualmente, para O:
Estos cuadrados de los intervalos, en el caso particular de la caída de la manzana, serán para o:
(ya que para él dx=dy=dz=0) y para O:
(suponiendo que la caída es vertical y que por tanto en el sistema de referencia de O dX = dY= 0)
La Teoría de la Relatividad establece, en función del movimiento relativo entre los dos observadores o y O, la posible relación entre (ds)2 y (dS)2. Aplicando dicha teoría, se puede calcular la relación entre los desplazamientos y los tiempos, medidos por el observador o y los medidos por el observador O, para la caída de la manzana.
Antes de calcular la relación pretendida entre los cuadrados de los intervalos en el caso particular de la caída de la manzana, vamos a detenernos un momento en estudiar esta relación en el caso completamente general para aplicar, después, las conclusiones obtenidas a nuestro caso concreto. Para este análisis previo en el caso general pensemos en un cambio de variables en las ecuaciones [5] y [6] haciendo, respectivamente:
y
Con estos cambios de variables se puede escribir, de forma condensada, que:
y que:
Conviene generalizar las ecuaciones [9] y [10], por un lado, y las [7] y [8], por otro, recordando que, al trabajar sobre superficies curvas en los respectivos sistemas de referencia, las coordenadas son coordenadas curvilíneas sobre las correspondientes superficies curvas. En este punto Einstein, aconsejado por Grossman, se apoyó en la geometría diferencial desarrollada por Gauss y, posteriormente, generalizada por Riemann puesto que:
- - Gauss había estudiado la geometría diferencial sobre superficies curvas en el espacio tridimensional de Euclides considerando que cada punto sobre una superficie estaba caracterizado por dos coordenadas u1 y u2 curvilíneas sobre dicha superficie.
- - Riemann había generalizado todas las ideas de Gauss a un espacio de cualquier número de coordenadas u1, u2 … … … un y, por lo tanto, proporcionó la geometría a utilizar en los espacios temporales de cuatro dimensiones.
Pueden resumirse las aportaciones de Gauss y de Riemann diciendo que:
- - Gauss había encontrado que la distancia, medida sobre la superficie curva en el espacio x, y, z, entre dos puntos con diferencias entre las coordenadas curvilíneas du1 y d u2 venía determinada, para un observador ajeno a la superficie, por la expresión:
- - Riemann, extrapolando las conclusiones de Gauss, permitió a Einstein decir que, en los espacios temporales de cuatro dimensiones, también el intervalo entre los puntos P y P+dP del espacio-tiempo x, y, z, ct visto en el sistema de referencia X, Y, Z, cT valdrá:
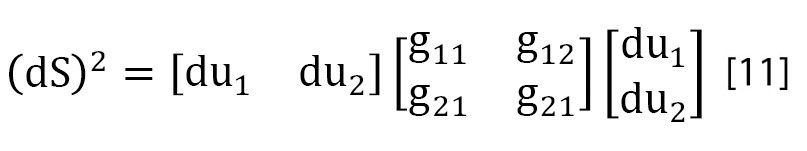
Desarrollando la ecuación [11] se puede escribir que:
sabiendo que g11, g12 = g21 y g22 dependen únicamente de las coordenadas curvilíneas del punto P desde el que se pretenda calcular da distancia entre los dos puntos P y P+dP de coordenadas curvilíneas respectivas u1, u2 y u1+du1, u2+du2.
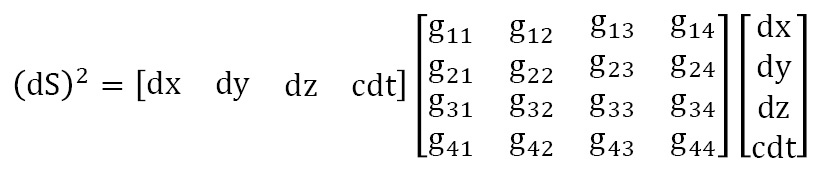
siendo

un tensor en el que cada una de sus dieciséis componentes (simétricas ya que gik=gki) es función de las cuatro coordenadas curvilíneas del punto P.
Esta ecuación en forma condensada quedaría reducida a:
siendo i, k = x, y, z, ct.
Puede concretarse todo lo anterior diciendo que:
- - El tensor (llamado tensor de los potenciales de Einstein) representa la métrica con la que el observador O mide, en su propio sistema de referencia X, Y, Z, cT, el cuadrado del intervalo medido por el observador o en su sistema de referencia x, y, z, ct.
- - Cada una de las componentes de este tensor depende, en cada punto de x, y, z, ct, del movimiento relativo entre el sistema de referencia x, y, z, ct, en el que está ubicado el observador o, respecto al sistema de referencia X, Y, Z, cT, asociado al observador O debiendo tener presente que:
- -En el caso de la Teoría de la Relatividad Especial, en que dicho movimiento relativo es simplemente una traslación uniforme en el espacio y constante en el tiempo, este tensor es el tensor unitario en todos los puntos por los que vaya pasando un punto material que se moviera en x, y, z, ct.
- - En el caso de la Teoría de la Relatividad General, si dicho movimiento tiene alguna aceleración, cada una de las componentes del tensor es diferente en los distintos puntos y depende, además, de la curvatura de la superficie en cada uno de dichos puntos.
- - El punto material que, en la representación matemática se mueve a lo largo de una geodésica sobre una superficie curva en el espacio-tiempo x, y, z, ct, es la manzana.
- -La curvatura de la superficie sobre la que se mueve la manzana está determinada por la masa de la Tierra.
- - El cuadrado del intervalo entre un punto P de la geodésica y otro punto P+dP de la misma vale para O:
- - Como en este caso se trata de un campo gravitatorio muy débil, comparado con los posibles campos gravitatorios ante masas grandísimas como las existentes en las proximidades, por ejemplo, de los agujeros negros, Einstein propuso para el tensor que relaciona los valores de los cuadrados del intervalo (para el observador O y para el otro observador o) la suma del tensor unitario y otro tensor también de dieciséis componentes simétricas εγij siendo ε una cantidad constante aunque muy pequeña.
- - En Mecánica Clásica, un punto material de masa m se mueve en un campo gravitatorio (en el espacio de Euclides y libre de otra acción exterior) cayendo en línea recta y según la dirección z de tal manera que la variación por unidad de tiempo de su energía cinética procede de la variación, también por unidad de tiempo, del potencial escalar del campo gravitatorio. Es decir:
- - En la teoría relativista de Einstein un punto material (nuestra manzana, por ejemplo) se mueve bajo un conjunto de circunstancias muy diferentes; citemos entre ellas:
- - En la representación matemática el punto material se mueve a lo largo de una geodésica ⎡ sobre una superficie curva en el espacio cuadrimensional x, y, z, ct.
- - En el cálculo no se introduce la acción de la gravedad ya que ésta ha sido sustituida por la aceleración del sistema de referencia x, y, z, ct respecto al sistema de referencia X, Y, Z, cT.
- - Por desplazarse sobre una superficie curva los sistemas de referencia para cada componente de su velocidad van cambiando al pasar de un punto a otro.
- - En cada punto de la geodésica puede definirse un cuadrivector velocidad con una componente en cada una de las coordenadas curvilíneas.
- - En lugar de tomar el tiempo como parámetro de referencia para formular el movimiento de la manzana, se ha de considerar el intervalo como dicho parámetro de referencia.
- - El estudio matemático de la gravedad puede hacerse considerando que la masa M de la Tierra determina una curvatura en cada punto de la representación del espacio-tiempo x, y, z, ct en que se mueve la manzana. Esta curvatura permite calcular las componentes del tensor gik de los potenciales de Einstein en dicho punto y estas componentes de gik miden, para cada uno de nosotros, el movimiento (la caída) de la manzana.
- - La ecuación [25], que relaciona el movimiento de una señal cualquiera (por medio de g44) con el potencial gravitatorio (dado por Φ) en el punto por donde se mueva la señal, justifica el cambio de frecuencia de una señal cuando abandona el Sol, con un potencial gravitatorio ΦS, y cuando la misma llega a la Tierra, con un campo gravitatorio ΦT < < ΦS. Así Einstein dio respuesta a la desviación hacia el rojo de cualquier emisión cuando pasa de un potencial gravitatorio a otro potencial gravitatorio menor. Esta desviación no tenía explicación satisfactoria para la Física Teórica antes de las geniales, aunque a veces aparentemente extrañas, conclusiones de Einstein.
Aplicación a la caída de la manzana
En nuestro caso de la caída de la manzana concurren las siguientes circunstancias particulares:
y para o:
Por lo tanto, la relación entre el cuadrado del intervalo de un desplazamiento infinitesimal de la manzana visto por Newton y el mismo cuadrado del intervalo visto por el observador solidario a la manzana vendría dada, de acuerdo con la extrapolación de Riemann a las conclusiones de Gauss, por:
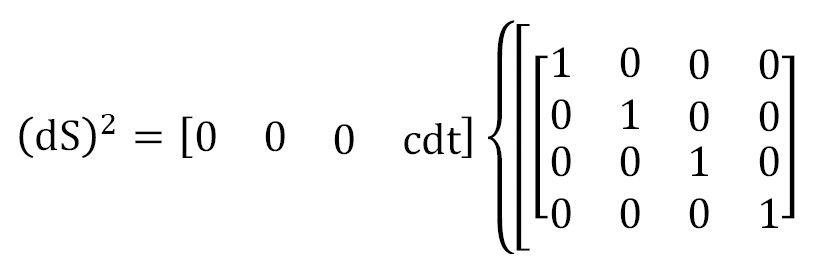
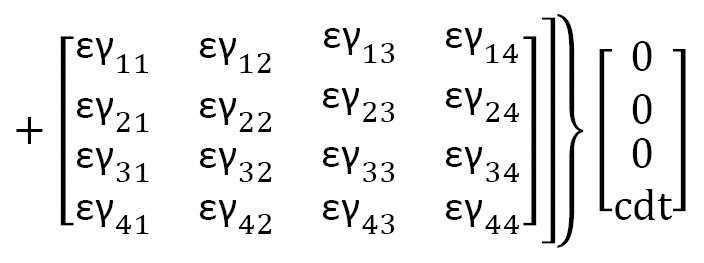
y operando:
Si dividimos la expresión anterior por dt2 tenemos:
Por otra parte y de acuerdo con la respuesta de Einstein, en representación matemática, la manzana se mueve en el sistema de referencia x, y, z, ct (sometido a la aceleración g respecto al sistema de referencia X, Y, Z, cT) libre de acciones exteriores y, por lo tanto, a lo largo de una geodésica ⎡ sobre una superficie curva en el espacio-tiempo x, y, z, ct. Para estudiar con cierto detenimiento este movimiento y compararlo con el movimiento preconizado mediante la Teoría de Campos según los criterios de la Mecánica Clásica pensemos que:
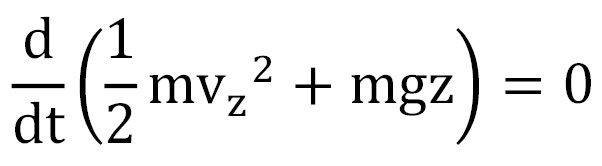
y desarrollando esta ecuación:
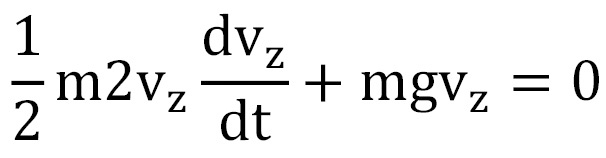
Eliminando factores comunes y teniendo en cuenta el signo de vz podemos decir que:
Como consecuencia de todo lo anterior, la ecuación [18] con el potencial escalar g se convierte, en cada punto de la geodésica del movimiento de la manzana, en:
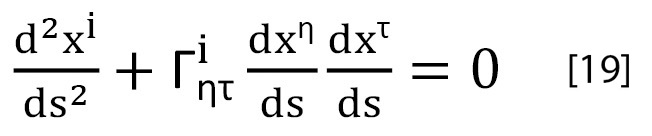
ecuación en la que:
xi es la componente del desplazamiento del punto material en cada punto y sobre cada una de las cuatro coordenadas al desplazarse el punto material (la manzana) a lo largo de la geodésica ⎡.
xη y, análogamente, xτ representa también cada una de las cuatro componentes del desplazamiento del punto material y en cada punto de la geodésica.
![]() representa la variación de la componente xi en función de la variación (en la unidad de intervalo) en cada punto de cada una de las componentes del desplazamiento a lo largo de ⎡.
representa la variación de la componente xi en función de la variación (en la unidad de intervalo) en cada punto de cada una de las componentes del desplazamiento a lo largo de ⎡.
A partir de [19], pasando al parámetro de referencia tiempo, se puede obtener, por un lado, la correlación entre la ecuación del movimiento a la luz de la Mecánica Relativista y bajo la óptica de la Mecánica Clásica y, por otro, (ver apartado siguiente) los valores de los potenciales correspondientes a cada punto de la geodésica. En efecto, para cambiar de parámetro, la ecuación [19] se transformará en:
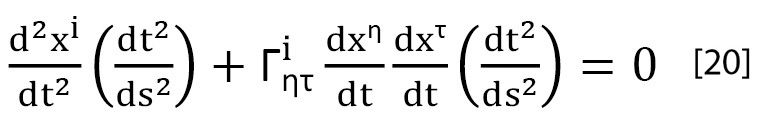
Y teniendo en cuenta la ecuación [17] se puede escribir que:
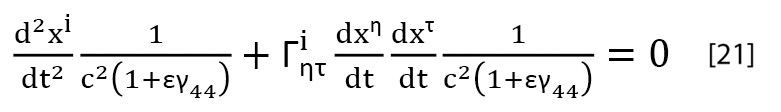
Ahora bien, en el caso de la caída de la manzana, ![]()
es nulo excepto cuando
luego [21] se convierte en:
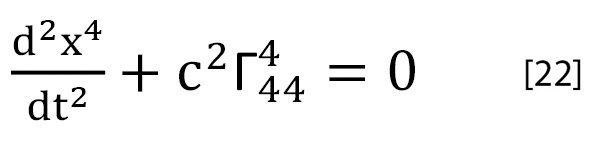
ecuación en la Mecánica Relativista para la caída de la manzana equivalente a la ecuación [18] en la Mecánica Clásica.
Relación entre la respuesta de Einstein y la propuesta de Newton
En la propuesta de Newton (aplicando la posterior Teoría de Campos) se obtenía, para la caída de la manzana en el espacio X, Y, Z de Euclides, que:
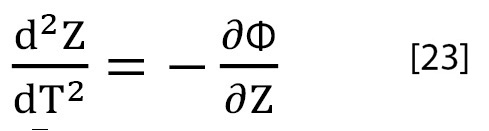
mientras que con la Teoría de la Relatividad General la ecuación [22], en el mismo caso de la caída de la manzana, se puede expresar diciendo que
pero como quiera que
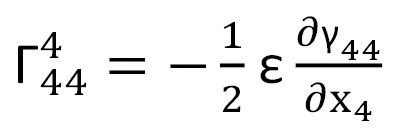
(esto está fuera del alcance de este artículo y se deduce fácilmente a partir de los símbolos de Christoffel), dicha ecuación [22] alcanzará la forma:
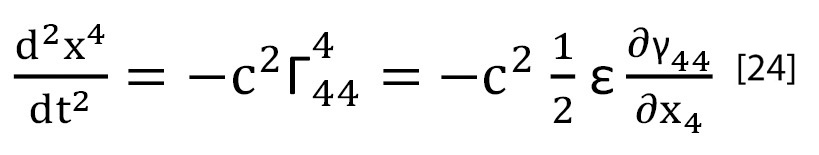
luego, comparando [23] y [24], puede escribirse que:
y como
la relación entre la componente del tensor de los potenciales de Einstein y el potencial gravitatorio vendrá dada por:
Conclusiones
De todo lo anterior podemos deducir, al relacionar la genial respuesta relativista de Einstein con la propuesta determinista de Newton, entre otras muchas posibles, las dos conclusiones siguientes:



